
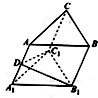
 在斜三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,∠AA1B=∠AA1C1=60°,∠BB1C1=90°,侧棱长AA1=3.
在斜三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,∠AA1B=∠AA1C1=60°,∠BB1C1=90°,侧棱长AA1=3.分析 (1)利用三角形面积公式求出上下底面的面积,由平行四边形面积公式求出侧面ABB1A1和ACC1A1的面积,再由矩形面积公式求出侧面BCC1B1的面积得答案;
(2)由${V_{棱柱}}={S_{△{B_1}D{C_1}}}•A{A_1}$,可得AA1⊥平面B1DC1,由已知求解直角三角形可得等腰三角形B1DC1的边长,进一步求其面积,代入棱柱体积公式得答案.
解答 解:(1)由题意知,斜三棱柱ABC-A1B1C1的底面是一个等腰直角三角形,且AB=AC=2,
∴BC=2$\sqrt{2}$,
∴${S}_{△ABC}={S}_{△{A}_{1}{B}_{1}{C}_{1}}=\frac{1}{2}×2×2=2$,
∵∠AA1B1=∠AA1C1=60°,AB=AC=2,AA1=3,
∴${S}_{四边形AB{B}_{1}{A}_{1}}={S}_{四边形AC{C}_{1}{A}_{1}}$=$2×3×sin60°=3\sqrt{3}$,
又∵∠BB1C1=90°,∴侧面BB1C1C为矩形,
∴${S}_{矩形B{B}_{1}{C}_{1}C}=3×2\sqrt{2}=6\sqrt{2}$.
∴斜三棱柱ABC-A1B1C1的表面积S=$2×2+2×3\sqrt{3}+6\sqrt{2}=4+6(\sqrt{2}+\sqrt{3})$;
(2)由题意,得AA1⊥平面B1DC1,
∵B1D?平面B1DC1,∴AA1⊥B1D,
又∵∠DA1B1=60°,A1B1=2,∴${B}_{1}D=\sqrt{3}$,同理$D{C}_{1}=\sqrt{3}$,
∴${V}_{棱柱}={S}_{△{B}_{1}D{C}_{1}}•A{A}_{1}=\frac{1}{2}×2\sqrt{2}×\sqrt{3-2}×3=3\sqrt{2}$.
点评 本题考查柱、锥、台体表面积与体积的求法,考查空间想象能力和思维能力,是中档题.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:解答题
 已知函数$f(x)=\left\{\begin{array}{l}{\sqrt{2}^x},x∈[0,2]\\ \frac{4}{x},x∈(2,4].\end{array}\right.$
已知函数$f(x)=\left\{\begin{array}{l}{\sqrt{2}^x},x∈[0,2]\\ \frac{4}{x},x∈(2,4].\end{array}\right.$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sinx | B. | y=cosx | C. | y=|sinx| | D. | y=|cosx| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com