
分析 (1)利用函数y=ax与y=loga(x+1)具有相同的单调性,得出f(x)在[0,1]上具有单调性,列出方程f(0)+f(1)=a,求出a的值;
(2)根据任意x∈[1,2],不等式Φ(x)+logam≥0恒成立,转化为m>0且m2≤$\frac{\sqrt{1+{x}^{2}}}{x}$,构造函数g(x)=$\frac{\sqrt{1{+x}^{2}}}{x}$,x∈[1,2],求出g(x)的最小值g(x)min,由此求出m的取值范围.
解答 解:(1)∵y=ax与y=loga(x+1)具有相同的单调性,
∴f(x)=ax+loga(x+1)在[0,1]上单调,
∴f(0)+f(1)=a,
即a0+loga1+a1+loga2=a,
化简得1+loga2=0,解得a=$\frac{1}{2}$;
(2)∵函数Φ(x)=loga$\frac{mx}{\sqrt{1+{x}^{2}}}$,
对任意x∈[1,2],不等式Φ(x)+logam≥0恒成立,
即${log}_{\frac{1}{2}}$$\frac{mx}{\sqrt{1{+x}^{2}}}$+${log}_{\frac{1}{2}}$m≥0恒成立,
∴${log}_{\frac{1}{2}}$$\frac{{m}^{2}x}{\sqrt{1{+x}^{2}}}$≥0恒成立,且m>0;
∴0<$\frac{{m}^{2}x}{\sqrt{1{+x}^{2}}}$≤1,
即m2≤$\frac{\sqrt{1+{x}^{2}}}{x}$,
设g(x)=$\frac{\sqrt{1{+x}^{2}}}{x}$,x∈[1,2],
∴g(x)=$\sqrt{\frac{1}{{x}^{2}}+1}$,
当x∈[1,2]时,$\frac{1}{x}$∈[$\frac{1}{2}$,1],
∴$\frac{1}{{x}^{2}}$+1∈[$\frac{5}{4}$,2];
∴g(x)的最小值是g(x)min=g(2)=$\frac{\sqrt{5}}{2}$;
令m2≤$\frac{\sqrt{5}}{2}$,
解得-$\frac{\root{4}{20}}{2}$≤m≤$\frac{\root{4}{20}}{2}$,
又m>0,
∴m的取值范围是0<m≤$\frac{\root{4}{20}}{2}$.
点评 本题主要考查了指数函数与对数函数的单调性应用问题,也考查了不等式恒成立与函数的最值问题,是综合性题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
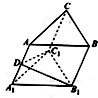 在斜三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,∠AA1B=∠AA1C1=60°,∠BB1C1=90°,侧棱长AA1=3.
在斜三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,∠AA1B=∠AA1C1=60°,∠BB1C1=90°,侧棱长AA1=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
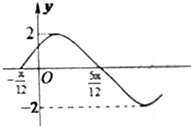 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com