
分析 根据题意,“渐升数”中不能有0,则在其他9个数字中任取4个,每种取法对应一个“渐升数”,再确定1在首位、2在百位;3在百位,4在十位,5在十位“渐升数”的个数,即可得出结论.
解答 解:根据题意,“渐升数”中不能有0,则在其他9个数字中任取4个,每种取法对应一个“渐升数”.
对于这些“渐升数”,1在首位、2在百位的有${C}_{7}^{2}$=21个;
1在首位、3在百位,4在十位的有5个,1在首位、3在百位,5在十位的有4个
故第30个“渐升数”为1359.
点评 本题考查排列、组合的应用,关键是理解“渐升数”的含义,其次要注意0不能在首位,即“渐升数”中不能有0,属于中档题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<0} | B. | {x|x≥1} | C. | {x|x>0} | D. | {x|x>-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
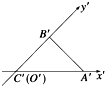 水平放置的△ABC的斜二测直观图△A′B′C′如图所示,已知A′C′=3,B′C′=2,则△ABC的面积为( )
水平放置的△ABC的斜二测直观图△A′B′C′如图所示,已知A′C′=3,B′C′=2,则△ABC的面积为( )| A. | 6 | B. | 3 | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $3\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ①④ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
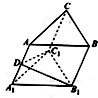 在斜三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,∠AA1B=∠AA1C1=60°,∠BB1C1=90°,侧棱长AA1=3.
在斜三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,∠AA1B=∠AA1C1=60°,∠BB1C1=90°,侧棱长AA1=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com