
分析 (1)由条件可得g(θ)=sin2θ-m(3-cosθ),从而求得$g(\frac{π}{2})$的值.
(2)根据g(θ)=-${(cosθ-\frac{m}{2})}^{2}$+$\frac{{m}^{2}}{4}$-3m+1,cosθ∈[0,1],利用二次函数的性质,分类讨论求得当g(θ)的最大值为4时,m的值.
解答 解:(1)∵行列式$|\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{{a}_{4}}\end{array}|$=a1a4-a2a3,函数g(θ)=$|\begin{array}{l}{sinθ}&{3-cosθ}\\{m}&{sinθ}\end{array}|$=sin2θ-m(3-cosθ) (其中$0≤θ≤\frac{π}{2}$).
∴$g(\frac{π}{2})$=${sin}^{2}\frac{π}{2}$-m(3-cos$\frac{π}{2}$)=1-3m.
(2)∵函数g(θ)=sin2θ-m(3-cosθ)=1-cos2θ+mcosθ-3m=-${(cosθ-\frac{m}{2})}^{2}$+$\frac{{m}^{2}}{4}$-3m+1.
∵$0≤θ≤\frac{π}{2}$,∴cosθ∈[0,1].
当$\frac{1}{2}$m∈[0,1]时,可得当cosθ=$\frac{m}{2}$时,g(θ)的最大值为4,即 $\frac{{m}^{2}}{4}$-3m+1=4,求得m=6+4$\sqrt{3}$ (舍去)或m=6-4$\sqrt{3}$(舍去).
当$\frac{1}{2}$m<0时,可得当cosθ=0时,g(θ)的最大值为1-3m=4,∴m=-1.
$\frac{1}{2}m$>1时,可得当cosθ=1时,g(θ)的最大值为m-3m=-2m=4,∴m=-2(舍去).
综上可得,m=-1.
点评 本题主要考查新定义,余弦函数的定义域和值域,二次函数的性质,体现了分类讨论的数学思想,属于中档题.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
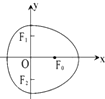 由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)合成的曲线称作“果圆”,如图所示,其中a2=b2+c2,a>b>c>0.由右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的焦点F0和左椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)的焦点F1,F2确定的△F0F1F2叫做果圆的焦点三角形,若果圆的焦点三角形为锐角三角形,则右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的离心率的取值范围为( )
由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)合成的曲线称作“果圆”,如图所示,其中a2=b2+c2,a>b>c>0.由右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的焦点F0和左椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)的焦点F1,F2确定的△F0F1F2叫做果圆的焦点三角形,若果圆的焦点三角形为锐角三角形,则右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的离心率的取值范围为( )| A. | ($\frac{1}{3}$,1) | B. | ($\frac{\sqrt{2}}{3}$,1) | C. | ($\frac{\sqrt{3}}{3}$,1) | D. | (0,$\frac{\sqrt{3}}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com