
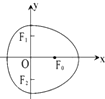
 由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)合成的曲线称作“果圆”,如图所示,其中a2=b2+c2,a>b>c>0.由右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的焦点F0和左椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)的焦点F1,F2确定的△F0F1F2叫做果圆的焦点三角形,若果圆的焦点三角形为锐角三角形,则右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的离心率的取值范围为( )
由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)合成的曲线称作“果圆”,如图所示,其中a2=b2+c2,a>b>c>0.由右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的焦点F0和左椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)的焦点F1,F2确定的△F0F1F2叫做果圆的焦点三角形,若果圆的焦点三角形为锐角三角形,则右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的离心率的取值范围为( )| A. | ($\frac{1}{3}$,1) | B. | ($\frac{\sqrt{2}}{3}$,1) | C. | ($\frac{\sqrt{3}}{3}$,1) | D. | (0,$\frac{\sqrt{3}}{3}$) |
分析 根据“果圆”关于x轴对称,得到△F1F0F2是以F1F2为底面的等腰三角形,从而可得:若△F0F1F2为锐角三角形,则|0F0|>|0F1|.由此建立关于a、b、c的不等式,结合椭圆离心率的公式与离心率的取值范围解此不等式,即可算出右椭圆离心率的取值范围.
解答 解:连结F0F1、F0F2,根据“果圆”关于x轴对称,可得△F1F0F2是以F1F2为底面的等腰三角形,
∵△F0F1F2是锐角三角形,
∴等腰△F0F1F2的顶角为锐角,即∠F1F0F2∈(0,$\frac{π}{2}$).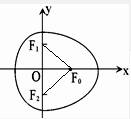
由此可得|0F0|>|0F1|,
∵|0F0|、|0F1|分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0),$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)的半焦距,
∴c>$\sqrt{{b}^{2}-{c}^{2}}$,平方得c2>b2-c2,
又∵b2=a2-c2,
∴c2>a2-2c2,解得:3c2>a2,
∴3•($\frac{c}{a}$)2>1,解之得$\frac{c}{a}$>$\frac{\sqrt{3}}{3}$.
∵右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的离心率e=$\frac{c}{a}$∈(0,1),
∴离心率e的范围为($\frac{\sqrt{3}}{3}$,1).
故答案选:C
点评 本题给出“果圆”满足的条件,考查椭圆离心率的取值范围,着重考查了椭圆的标准方程与简单几何性质、不等式的解法等的综合应用,属于中档题.


科目:高中数学 来源: 题型:解答题
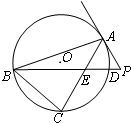 如图,△ABC是圆O的内接三角形,PA是圆O的切线,A为切点,PB交AC于点E,交圆O于点D,若PE=PA,∠ABC=60°,且PD=1,PB=9,求EC.
如图,△ABC是圆O的内接三角形,PA是圆O的切线,A为切点,PB交AC于点E,交圆O于点D,若PE=PA,∠ABC=60°,且PD=1,PB=9,求EC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π-1}{4}$ | B. | $\frac{π-1}{2}$ | C. | $\frac{π-2}{4}$ | D. | $\frac{π-2}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
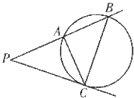 如图,过点P作圆的切线PC,切点为C,过点P的直线与圆交于点A、B,$PA=2\sqrt{2}$.
如图,过点P作圆的切线PC,切点为C,过点P的直线与圆交于点A、B,$PA=2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com