
分析 (1)利用等比数列的通项公式与求和公式即可得出.
(2)利用等比数列的求和公式即可得出.
解答 解:(1)若q=1,则S4=2S2,与已知矛盾,∴q≠1,
∴$\left\{\begin{array}{l}{S_2}=\frac{{{a_1}(1-{q^2})}}{1-q}=3\\{S_4}=\frac{{{a_1}(1-{q^4})}}{1-q}=15\end{array}\right.$
又q>0,解得$\left\{\begin{array}{l}{a_1}=1\\ q=2\end{array}\right.$
∴${a_n}={2^{n-1}}$.
(2)由(1),可以求得${S_n}={2^n}-1$,
于是${T_n}={2^1}-1+{2^2}-1+…+{2^n}-1={2^1}+{2^2}+…+{2^n}-1-1-…-1$=$\frac{{2(1-{2^n})}}{1-2}-n={2^{n+1}}-n-2$.
点评 本题考查了等比数列的通项公式及其求和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
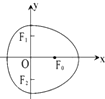 由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)合成的曲线称作“果圆”,如图所示,其中a2=b2+c2,a>b>c>0.由右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的焦点F0和左椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)的焦点F1,F2确定的△F0F1F2叫做果圆的焦点三角形,若果圆的焦点三角形为锐角三角形,则右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的离心率的取值范围为( )
由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)合成的曲线称作“果圆”,如图所示,其中a2=b2+c2,a>b>c>0.由右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的焦点F0和左椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)的焦点F1,F2确定的△F0F1F2叫做果圆的焦点三角形,若果圆的焦点三角形为锐角三角形,则右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的离心率的取值范围为( )| A. | ($\frac{1}{3}$,1) | B. | ($\frac{\sqrt{2}}{3}$,1) | C. | ($\frac{\sqrt{3}}{3}$,1) | D. | (0,$\frac{\sqrt{3}}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 2π | C. | 3π | D. | $\frac{3π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 转速x(转/秒) | 2 | 4 | 5 | 6 | 8 |
| 每小时生产有缺点的零件数y(件) | 10 | 30 | 60 | 50 | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com