
| A. | $\frac{1}{2}$ | B. | 2 | C. | 0 | D. | 1 |
分析 构造函数,求导,根据导数求出函数的最小值,即可求出k的范围,问题得以解决.
解答 解:设f(x)=4x3-3x2+$\frac{1}{4}$,x∈[0,2]
则f′(x)=12x2-6x,
令f′(x)=0,得x1=0,x2=$\frac{1}{2}$,
当f′(x)>0时,即$\frac{1}{2}$<x≤2,函数单调递增,
当f′(x)≤0时,即0≤x≤$\frac{1}{2}$,函数单调递减,
∴f(x)min=f($\frac{1}{2}$)=4×$\frac{1}{8}$-3×$\frac{1}{4}$+$\frac{1}{4}$=0,
∴k≤0,
故实数k的最大值为0,
故选:C.
点评 本题考查利用导数求函数在闭区间上最值的应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{π-1}{4}$ | B. | $\frac{π-1}{2}$ | C. | $\frac{π-2}{4}$ | D. | $\frac{π-2}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
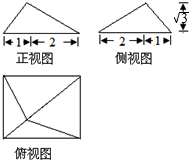 某四棱锥的三视图如图所示(单位:cm),则该四棱锥的表面积是( )
某四棱锥的三视图如图所示(单位:cm),则该四棱锥的表面积是( )| A. | $(13+3\sqrt{7})c{m^2}$ | B. | $(12+4\sqrt{3})c{m^2}$ | C. | $(18+3\sqrt{7})c{m^2}$ | D. | $(15+3\sqrt{7})c{m^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若xy=0,则x=0”的否命题为“若xy≠0,则x≠0” | |
| B. | 命题“?x∈R,x2-x-1≤0”的否定是“$?{x_0}∈{R},{x_0}^2-{x_0}-1>0$” | |
| C. | 若p,q均为假命题,则p∧q为假命题 | |
| D. | 命题“?x∈[1,2],x2-a≤0”为真命题的一个充分不必要条件是a≥4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com