
| 房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
分析 (1)根据表中所给的五对数据,在平面直角坐标系中描出这五个点,得到这组数据的散点图.
(2)根据表中所给的数据,求出横标和纵标的平均数,把求得的数据代入求线性回归方程的系数的公式,利用最小二乘法得到结果,写出线性回归方程.
(3)根据第二问求得的线性回归方程,代入所给的x的值,预报出销售价格的估计值,这个数字不是一个准确数值.
解答 解:(1)数据对应的散点图如图所示: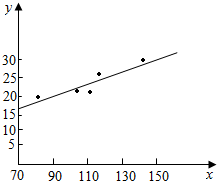
(2)$\overline{x}$=109,$\overline{y}$=23.2,$\sum_{i=1}^{5}$${{x}_{i}}^{2}$=60975,$\sum_{i=1}^{5}{x}_{i}{y}_{i}$=115×24.8+110×21.6+80×18.4+135×29.2+105×22=12952,
则$\stackrel{∧}{b}$=$\frac{12952-5×109×23.2}{60975-5×10{9}^{2}}$≈0.1962
$\stackrel{∧}{a}$=23.2-0.1962×109≈1.8142,
故所求回归直线方程为$\stackrel{∧}{y}$=0.1962x+1.8142;
(3)据(2),当x=150m2时,销售价格的估计值为:$\stackrel{∧}{y}$=0.1962×150+1.8142=31.2442(万元)
点评 本题考查线性回归方程的求法和应用,解决本题的关键是利用最小二乘法求线性回归方程的系数时,不要弄错数据.


科目:高中数学 来源: 题型:选择题
| A. | (0,ln3) | B. | (0,2) | C. | (0,e) | D. | (0,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
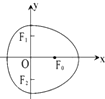 由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)合成的曲线称作“果圆”,如图所示,其中a2=b2+c2,a>b>c>0.由右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的焦点F0和左椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)的焦点F1,F2确定的△F0F1F2叫做果圆的焦点三角形,若果圆的焦点三角形为锐角三角形,则右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的离心率的取值范围为( )
由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)合成的曲线称作“果圆”,如图所示,其中a2=b2+c2,a>b>c>0.由右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的焦点F0和左椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)的焦点F1,F2确定的△F0F1F2叫做果圆的焦点三角形,若果圆的焦点三角形为锐角三角形,则右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的离心率的取值范围为( )| A. | ($\frac{1}{3}$,1) | B. | ($\frac{\sqrt{2}}{3}$,1) | C. | ($\frac{\sqrt{3}}{3}$,1) | D. | (0,$\frac{\sqrt{3}}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
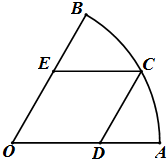 如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,半径为R,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在弧AB上选一点C,过C修建与OB平行的小路CD,与OA平行的小路CE,设∠COA=θ,
如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,半径为R,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在弧AB上选一点C,过C修建与OB平行的小路CD,与OA平行的小路CE,设∠COA=θ,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | 0 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com