
分析 根据条件即可得出f(x3-x2+a)≥f(1),而f(x)为偶函数,从而得出f(|x3-x2+a|)≥f(1),根据单调性即可得出|x3-x2+a|≤1,进而得出-x3+x2-1≤a≤-x3+x2+1,而x∈[0,1].可设g(x)=-x3+x2+1,h(x)=-x3+x2-1,然后求导数,根据导数符号判断g(x),h(x)的单调性,进而得出g(x)的最小值,h(x)的最大值,从而得出a的取值范围.
解答 解:f(x)是R上的偶函数;
∴f(-x3+x2-a)=f(x3-x2+a);
∴由f(x3-x2+a)+f(-x3+x2-a)≥2f(1)得,2f(x3-x2+a)≥2f(1);
∴f(x3-x2+a)≥f(1);
∴f(|x3-x2+a|)≥f(1);
又f(x)在[0,+∞)上递减;
∴|x3-x2+a|≤1;
∴-1≤x3-x2+a≤1;
∴-x3+x2-1≤a≤-x3+x2+1对x∈[0,1]恒成立;
设g(x)=-x3+x2+1,h(x)=-x3+x2-1,则$g′(x)=h′(x)=-3x(x-\frac{2}{3})$;
∴$x∈[0,\frac{2}{3}]$时,g(x),h(x)都单调递增,x$∈(\frac{2}{3},1]$时,g(x),h(x)都单调递减;
∴h(x)的最大值为$f(\frac{2}{3})=-\frac{23}{27}$,g(x)的最小值为f(0)=1;
∴$-\frac{23}{27}≤a≤1$;
即实数a的取值范围为$[-\frac{23}{27},1]$.
故答案为:$[-\frac{23}{27},1]$.
点评 考查偶函数的定义,减函数的定义,绝对值不等式的解法,以及函数导数符号和函数单调性的关系,根据函数单调性求函数最值的方法,以及恒成立问题的处理方法.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | [0,2] | B. | (1,2] | C. | (1,18] | D. | [0,1]∪(1,18] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-∞,2] | C. | (-1,2] | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π-1}{4}$ | B. | $\frac{π-1}{2}$ | C. | $\frac{π-2}{4}$ | D. | $\frac{π-2}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
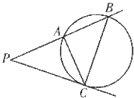 如图,过点P作圆的切线PC,切点为C,过点P的直线与圆交于点A、B,$PA=2\sqrt{2}$.
如图,过点P作圆的切线PC,切点为C,过点P的直线与圆交于点A、B,$PA=2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com