练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．设A={x|y=$\sqrt{2-x}$}，B={y|y=ln（1+x）}，则A∩B=（　　）
    A．（-1，+∞）B．（-∞，2]C．（-1，2]D．∅

    分析 分别求出集合A，B的范围，求出A、B的交集即可．

    解答 解：A={x|y=$\sqrt{2-x}$}={x|x≤2}，
    B={y|y=ln（1+x）}=R
    则A∩B=（-∞，2]，
    故选：B．

    点评 本题考查了集合的运算，考查二次根式以及对数函数的性质，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．下列命题错误的是（　　）
    A．两个随机变量的线性相关性越强，相关系数的绝对值越接近于1
    B．设ξ～N（0，σ2），且P（ξ＜-1）=$\frac{1}{4}$，则P（0＜ξ＜1）=$\frac{1}{4}$
    C．在残差图中，残差点分布的带状区域的宽带越狭窄，其模型拟合的精度越高
    D．已知函数f（x）可导，则“f′（x0）=0”是“x0是函数f（x）极值点”的充要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．复数z=（a2-9）+（a+3）i是纯虚数，则a=（　　）
    A．-3B．±3C．3D．∅

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知函数f（x）是定义在R上的偶函数，当x≥0时，f（x）=|ex-3|，若函数y=f（x）-k恰有4 个零点，则实数k的取值范围是（　　）
    A．（0，ln3）B．（0，2）C．（0，e）D．（0，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．执行如图所示的程序框图，如果运行结果为720，那么判断框中应填入（　　）
    A．k＜6？B．k＜7？C．k＞6？D．k＞7？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．近两年来，各大电视台都推出了由明星参与的游戏竞技类节目．高一某研究性学习小组在长沙某社区对50人进行第一时间收看该类节目与性别是否有关的收视调查，其中20名女性中有15名第一时间收看该类节目，30名男性中10名第一时间收看该类节目．
    （1）根据以上数据建立一个2×2列联表，并判断第一时间收看该类节目是否与性别有关？
    （2）该研究性学习小组共有A、B、C、D和E五名同学，五人分成两组模拟“撕名牌”的游戏，其中一组三人，一组两人，求A、B两同学分在同一组的概率．
    参考数据：${Χ^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．
    临界值表：
    P（Χ2≥k）0.1000.0500.0250.0100.0050.001
    k2.7063.8415.0246.6357.87910.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

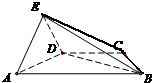    11．在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥BD，∠DAB=60°，AE⊥BD，CB=CD=AE=DE=1；
    （Ⅰ）求证：BD⊥平面AED；
    （2）求直线AB与平面BDE所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知定义在R上的偶函数f（x）在[0，+∞）上递减，若不等式f（x3-x2+a）+f（-x3+x2-a）≥2f（1）对x∈[0，1]恒成立，则实数a的取值范围为[$-\frac{23}{27}$，1]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

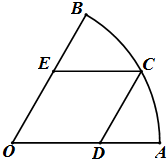    9．如图，某广场中间有一块扇形绿地OAB，其中O为扇形所在圆的圆心，半径为R，∠AOB=60°，广场管理部门欲在绿地上修建观光小路：在弧AB上选一点C，过C修建与OB平行的小路CD，与OA平行的小路CE，设∠COA=θ，
    （1）当θ=45°时，求CD；
    （2）θ为何值时，才能使得修建的道路CD与CE的总长最大，并说明理由．

    查看答案和解析>>

    同步练习册答案