
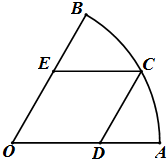
 如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,半径为R,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在弧AB上选一点C,过C修建与OB平行的小路CD,与OA平行的小路CE,设∠COA=θ,
如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,半径为R,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在弧AB上选一点C,过C修建与OB平行的小路CD,与OA平行的小路CE,设∠COA=θ,分析 (1)在△COD中,由已知及正弦定理可求CD.
(2)由已知及正弦定理可得$CD=\frac{{2\sqrt{3}}}{3}Rsinθ$,$OD=\frac{{2\sqrt{3}}}{3}Rsin({60°-θ})$,利用三角函数恒等变换的应用化简可得$CD+CE=\frac{{2\sqrt{3}}}{3}Rsin({θ+60°})$,结合范围θ+60°∈(60°,120°),利用正弦函数的性质可得结果.
解答 答:(1)在△COD中,∠COD=45°,∠ODC=120°,OC=R,
由正弦定理得:$\frac{CD}{sin∠COD}=\frac{OC}{sin∠ODC}$,
∴$CD=\frac{{\sqrt{6}}}{3}R$.
(2)在△COD中,由正弦定理得:$CD=\frac{{2\sqrt{3}}}{3}Rsinθ$,$OD=\frac{{2\sqrt{3}}}{3}Rsin({60°-θ})$,
∴$CD+CE=CD+OD=\frac{{2\sqrt{3}}}{3}Rsinθ+\frac{{2\sqrt{3}}}{3}Rsin({60°-θ})=\frac{{2\sqrt{3}}}{3}R({\frac{1}{2}sinθ+\frac{{\sqrt{3}}}{2}cosθ})$,
即:$CD+CE=\frac{{2\sqrt{3}}}{3}Rsin({θ+60°})$,
∵θ∈(0°,60°),
∴θ+60°∈(60°,120°),
所以,当θ=30°时,CD与CE的总长最大,最大值为$\frac{{2\sqrt{3}}}{3}R$.
点评 本题给出圆心角为60度的扇形场地,求修建道路CD与CE的总长最大值,着重考查了利用正弦定理解三角形、正弦函数的图象和性质等知识,考查了数形结合思想,属于中档题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-∞,2] | C. | (-1,2] | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
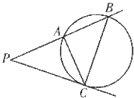 如图,过点P作圆的切线PC,切点为C,过点P的直线与圆交于点A、B,$PA=2\sqrt{2}$.
如图,过点P作圆的切线PC,切点为C,过点P的直线与圆交于点A、B,$PA=2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 房屋面积(m2) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
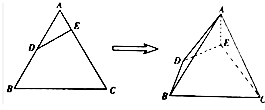 如图,已知△ABC为正三角形,D为AB的中点,E在AC上,且AE
如图,已知△ABC为正三角形,D为AB的中点,E在AC上,且AE查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
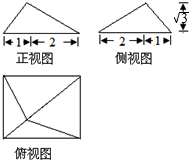 某四棱锥的三视图如图所示(单位:cm),则该四棱锥的表面积是( )
某四棱锥的三视图如图所示(单位:cm),则该四棱锥的表面积是( )| A. | $(13+3\sqrt{7})c{m^2}$ | B. | $(12+4\sqrt{3})c{m^2}$ | C. | $(18+3\sqrt{7})c{m^2}$ | D. | $(15+3\sqrt{7})c{m^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,+∞) | B. | (-∞,3) | C. | (-∞,3] | D. | (-∞,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com