
| A. | (3,+∞) | B. | (-∞,3) | C. | (-∞,3] | D. | (-∞,3) |
分析 求导数得到f′(x)=3x2-2ax+3,根据条件可得到f′(x)≥0在x∈[1,+∞)上恒成立,从而便可得出△≤0,或$\left\{\begin{array}{l}{△>0}\\{\frac{a}{2}<1}\\{f(1)≥0}\end{array}\right.$,这样即可解出a的范围,即得出实数a的取值范围.
解答 解:f′(x)=3x2-2ax+3;
∵f(x)在[1,+∞)上是增函数;
∴f′(x)≥0在x∈[1,+∞)上恒成立;
∴△=4a2-36≤0,或$\left\{\begin{array}{l}{△=4{a}^{2}-36>0}\\{\frac{a}{2}<1}\\{f(1)=1-a+3≥0}\end{array}\right.$;
解得-3≤a≤3,或a<-3;
∴a≤3;
∴实数a的取值范围是(-∞,3].
故选:C.
点评 考查函数单调性和函数导数符号的关系,基本初等函数的求导,二次函数符号和判别式△的关系,要熟悉二次函数的图象.


科目:高中数学 来源: 题型:解答题
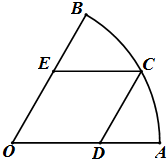 如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,半径为R,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在弧AB上选一点C,过C修建与OB平行的小路CD,与OA平行的小路CE,设∠COA=θ,
如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,半径为R,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在弧AB上选一点C,过C修建与OB平行的小路CD,与OA平行的小路CE,设∠COA=θ,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a-c=0且b-d≠0 | B. | a-c=0且b+d≠0 | C. | a+c=0且b+d≠0 | D. | a+c≠0且b+d=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 转速x(转/秒) | 2 | 4 | 5 | 6 | 8 |
| 每小时生产有缺点的零件数y(件) | 10 | 30 | 60 | 50 | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{625}{6}$ | B. | $\frac{250}{6}$ | C. | $\frac{375}{6}$ | D. | $\frac{125}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | [1,3] | C. | [0,3] | D. | [1,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com