
分析 求导函数,确定函数的单调性,可得函数的极值与端点函数值比较,即可得到结论.
解答 解:∵f(x)=x3-3x+1在[-3,2],
∴f'(x)=3x2-3,
由f'(x)=0得 x1=-1,x2=1
当x∈(-1,1)时,f'(x)<0,f(x)单调递减;
当x∈[-3,1),(1,2]时,f'(x)>0,f(x)单调递增.
∴x1=-1是函数f(x)的极大值点,x1=1是函数f(x)的极小值点,
计算函数在极小值和极大值点及区间端点的值,
得f(-1)=3,f(-3)=-17,f(1)=-3,f(2)=3,
∴f(x)=x3-3x+1在[-3,2]上的最大值是3,最小值是-17.
点评 本题考查导数知识的运用,考查函数的最值,考查学生的计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
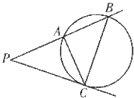 如图,过点P作圆的切线PC,切点为C,过点P的直线与圆交于点A、B,$PA=2\sqrt{2}$.
如图,过点P作圆的切线PC,切点为C,过点P的直线与圆交于点A、B,$PA=2\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
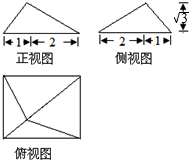 某四棱锥的三视图如图所示(单位:cm),则该四棱锥的表面积是( )
某四棱锥的三视图如图所示(单位:cm),则该四棱锥的表面积是( )| A. | $(13+3\sqrt{7})c{m^2}$ | B. | $(12+4\sqrt{3})c{m^2}$ | C. | $(18+3\sqrt{7})c{m^2}$ | D. | $(15+3\sqrt{7})c{m^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,+∞) | B. | (-∞,3) | C. | (-∞,3] | D. | (-∞,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com