
分析 (1)利用公式an=Sn-Sn-1得出{an}为等比数列,根据a1,a3+1,a4成等差数列列方程解出a1即可得出an;
(2)求出cn,使用错位相减法求和.
解答 解:(1)n≥2时,Sn-1=2an-1-a1,
∴an=Sn-Sn-1=2an-2an-1,即an=2an-1.
∴{an}是以2为公比的等比数列,
∵a1,a3+1,a4成等差数列,
∴a1+8a1=2(4a1+1),解得a1=2,
∴an=2n.
(2)bn=log22n=n,
∴cn=n•2n.
∴Tn=1•2+2•22+3•23+…+n•2n,
∴2Tn=1•22+2•23+3•24+…+n•2n+1,
∴-Tn=2+22+23+…+2n-n•2n+1=$\frac{2(1-{2}^{n})}{1-2}$-n•2n+1=(1-n)2n+1-2.
∴Tn=2+(n-1)2n+1.
点评 本题考查了数列通项公式的求法,错位相减法求和,属于中档题.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
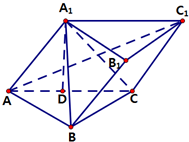 在斜三棱柱ABC-A1B1C1中,BC⊥CC1,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D.
在斜三棱柱ABC-A1B1C1中,BC⊥CC1,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a-c=0且b-d≠0 | B. | a-c=0且b+d≠0 | C. | a+c=0且b+d≠0 | D. | a+c≠0且b+d=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{625}{6}$ | B. | $\frac{250}{6}$ | C. | $\frac{375}{6}$ | D. | $\frac{125}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com