
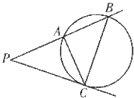
 如图,过点P作圆的切线PC,切点为C,过点P的直线与圆交于点A、B,$PA=2\sqrt{2}$.
如图,过点P作圆的切线PC,切点为C,过点P的直线与圆交于点A、B,$PA=2\sqrt{2}$.分析 (1)由弦切角定理,∠ABC=∠APC,可知△ACB∽△APC,根据三角形相似性质可知$\frac{PA}{AC}$=$\frac{AC}{AB}$,代入即可求得AC的长;
(2)设圆心到直线PB的距离为d,AB=2$\sqrt{4-{d}^{2}}$,根据切割定理可知PC2=PA•PB,代入即可求得d的值.
解答 解:(1)∵PC与圆相切,切点为C,
BC⊥PC,
由弦切角定理,∠ABC=∠ACP,
又∵由BC为圆的直径,
∠BAC=90°,
∴∠ACB=∠APC,
∴△ACB∽△APC,
$\frac{PA}{AC}$=$\frac{AC}{AB}$,即AC2=PA•AB=8,
∴AC=2$\sqrt{2}$;
(2)设圆心到直线PB的距离为d,
∴AB=2$\sqrt{4-{d}^{2}}$,
由切割定理可得:PC2=PA•PB,
即16=2$\sqrt{2}$(2$\sqrt{2}$+2$\sqrt{4-{d}^{2}}$),
解得:d=$\sqrt{2}$,
圆心到直线PB的距离$\sqrt{2}$.
点评 本题考查直线与圆的关系,考查弦切角定理,切割定理的应用及三角形相似的性质,考查数形结合思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
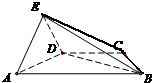 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥BD,∠DAB=60°,AE⊥BD,CB=CD=AE=DE=1;
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥BD,∠DAB=60°,AE⊥BD,CB=CD=AE=DE=1;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
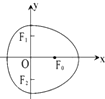 由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)合成的曲线称作“果圆”,如图所示,其中a2=b2+c2,a>b>c>0.由右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的焦点F0和左椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)的焦点F1,F2确定的△F0F1F2叫做果圆的焦点三角形,若果圆的焦点三角形为锐角三角形,则右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的离心率的取值范围为( )
由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)合成的曲线称作“果圆”,如图所示,其中a2=b2+c2,a>b>c>0.由右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的焦点F0和左椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)的焦点F1,F2确定的△F0F1F2叫做果圆的焦点三角形,若果圆的焦点三角形为锐角三角形,则右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的离心率的取值范围为( )| A. | ($\frac{1}{3}$,1) | B. | ($\frac{\sqrt{2}}{3}$,1) | C. | ($\frac{\sqrt{3}}{3}$,1) | D. | (0,$\frac{\sqrt{3}}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
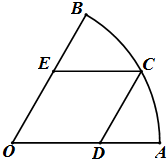 如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,半径为R,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在弧AB上选一点C,过C修建与OB平行的小路CD,与OA平行的小路CE,设∠COA=θ,
如图,某广场中间有一块扇形绿地OAB,其中O为扇形所在圆的圆心,半径为R,∠AOB=60°,广场管理部门欲在绿地上修建观光小路:在弧AB上选一点C,过C修建与OB平行的小路CD,与OA平行的小路CE,设∠COA=θ,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com