
| 转速x(转/秒) | 2 | 4 | 5 | 6 | 8 |
| 每小时生产有缺点的零件数y(件) | 10 | 30 | 60 | 50 | 80 |
分析 (1)先求出横标和纵标的平均数,代入求系数b的公式,利用最小二乘法得到系数,再根据公式求出a的值,写出线性回归方程,得到结果.
(2)预测每小时的产品中有缺点的零件为92个,利用回归方程,得到要求的机器允许的转数.
解答 解:(1)∵$\overline x=5$,$\overline y=46$,$\sum_{i=1}^{5}$xiyi=1380,$\sum_{i=1}^{5}{{x}_{i}}^{2}$=145.
∴$\stackrel{∧}{b}$=$\frac{1380-5×5×46}{145-5×5×5}$=11.5,$\widehata=\overline y-\widehatb\overline x=-11.5$
∴回归直线方程为:$\widehaty=11.5\widehatx-11.5$.-----------------(7分)
(2)令11.5x-11.5=92,解得x=9.…(10分)
点评 本题考查线性回归分析,考查线性回归方程,考查线性回归方程的应用,是一个综合题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,+∞) | B. | (-∞,3) | C. | (-∞,3] | D. | (-∞,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
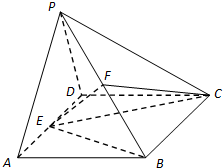 如图,已知四棱锥P-ABCD中,△PAD是边长为a的正三角形,平面PAD⊥平面ABCD,四边形ABCD是菱形,∠DAB=60°,E是AD的中点,F是PB的中点.
如图,已知四棱锥P-ABCD中,△PAD是边长为a的正三角形,平面PAD⊥平面ABCD,四边形ABCD是菱形,∠DAB=60°,E是AD的中点,F是PB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com