
分析 由题意画出图形,由已知求出cos∠PF1F2,再由余弦定理求得c得答案.
解答 解:如图,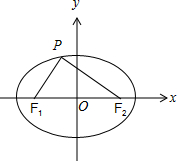
由tan$∠P{F}_{1}{F}_{2}=\frac{12}{5}$,得∠PF1F2为锐角,
且$\frac{sin∠P{F}_{1}{F}_{2}}{cos∠P{F}_{1}{F}_{2}}=\frac{12}{5}$,联立$si{n}^{2}∠P{F}_{1}F2+co{s}^{2}∠P{F}_{1}{F}_{2}=1$,
解得:cos∠PF1F2=$\frac{5}{13}$,
在△PF1F2中,有$|P{F}_{2}{|}^{2}=|P{F}_{1}{|}^{2}+4{c}^{2}-4c|P{F}_{1}|cos∠P{F}_{1}{F}_{2}$,
得$1{5}^{2}=1{3}^{2}+4{c}^{2}-4×13×\frac{5}{13}c$,解得c=-2(舍)或c=7.
又2a=|PF1|+|PF2|=13+15=28,得a=14,
∴$e=\frac{c}{a}=\frac{7}{14}=\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查椭圆的简单性质,考查余弦定理的应用,是中档题.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:解答题
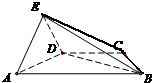 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥BD,∠DAB=60°,AE⊥BD,CB=CD=AE=DE=1;
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥BD,∠DAB=60°,AE⊥BD,CB=CD=AE=DE=1;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 100 | B. | 150 | C. | 120 | D. | 160 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
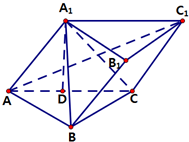 在斜三棱柱ABC-A1B1C1中,BC⊥CC1,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D.
在斜三棱柱ABC-A1B1C1中,BC⊥CC1,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com