
| A. | $\frac{π-1}{4}$ | B. | $\frac{π-1}{2}$ | C. | $\frac{π-2}{4}$ | D. | $\frac{π-2}{2}$ |
分析 根据几何概型,只要求出在两个区间内随机取两个数分别记为a,b,对应平面区域的面积,再求出满足条件a2+b2≤2对应的平面区域的面积,然后代入几何概型公式,即可求解.
解答 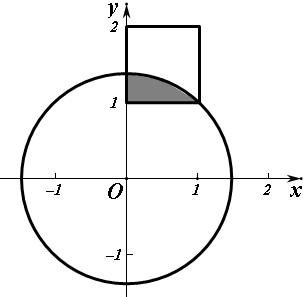 解:[0,1]上任取一数a,在[1,2]上任取一数b,则(a,b)点对应的区域如图中正方形所示
解:[0,1]上任取一数a,在[1,2]上任取一数b,则(a,b)点对应的区域如图中正方形所示
若a2+b2≤2,
则(a,b)点对应的区域在以原点为圆心,以$\sqrt{2}$为半径的圆上或圆内
如图中阴影部分所示,∵S正方形=1×1=1,
S阴影=$\frac{π•(\sqrt{2})^{2}}{8}-\frac{1}{2}$=$\frac{π}{4}$-$\frac{1}{2}$,
故在[-1,1]上任取一数a,在[1,2]上任取一数b,使得a2+b2≤2的概率P=2×$\frac{\frac{π}{4}-\frac{1}{2}}{1}$=$\frac{π-2}{2}$.
故选:D.
点评 本题考查几何概型;其概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.


科目:高中数学 来源: 题型:选择题
| A. | [3,+∞) | B. | [4,+∞) | C. | {2$\sqrt{3}$}∪[3,+∞) | D. | {2$\sqrt{2}$}∪[4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,ln3) | B. | (0,2) | C. | (0,e) | D. | (0,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(Χ2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
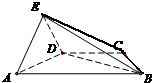 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥BD,∠DAB=60°,AE⊥BD,CB=CD=AE=DE=1;
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥BD,∠DAB=60°,AE⊥BD,CB=CD=AE=DE=1;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
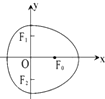 由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)合成的曲线称作“果圆”,如图所示,其中a2=b2+c2,a>b>c>0.由右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的焦点F0和左椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)的焦点F1,F2确定的△F0F1F2叫做果圆的焦点三角形,若果圆的焦点三角形为锐角三角形,则右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的离心率的取值范围为( )
由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)合成的曲线称作“果圆”,如图所示,其中a2=b2+c2,a>b>c>0.由右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的焦点F0和左椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x≤0)的焦点F1,F2确定的△F0F1F2叫做果圆的焦点三角形,若果圆的焦点三角形为锐角三角形,则右椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)的离心率的取值范围为( )| A. | ($\frac{1}{3}$,1) | B. | ($\frac{\sqrt{2}}{3}$,1) | C. | ($\frac{\sqrt{3}}{3}$,1) | D. | (0,$\frac{\sqrt{3}}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | 0 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com