
分析 根据题意,利用角度关系构建三角形,再利用正弦定理求各边长,即可得到周长.
解答 解:如图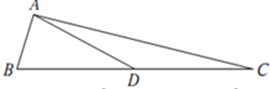 ,连接AD,∵∠B=75°,∠ADC=150°
,连接AD,∵∠B=75°,∠ADC=150°
∴∠BAD=75°
那么:$\frac{BD}{sin∠BAD}=\frac{AB}{sin∠BDA}$
即$\frac{\sqrt{6}+\sqrt{2}}{sin75°}=\frac{AB}{sin150°}$
解得:AB=2.
又∵BD=DC=$\sqrt{6+\sqrt{2}}$
∴BC=2$\sqrt{6}$+$2\sqrt{2}$.
所以:∠DAC=∠DCA=15°.
可得∠BAC=90°,
那么:AC=BC•cos∠BCA=4+2$\sqrt{3}$
因此:△ABC的周长为:BC+AC+AB=2+2$\sqrt{6}$+$2\sqrt{2}$+4+2$\sqrt{3}$=6+2($\sqrt{6}+\sqrt{2}+\sqrt{3}$)
故答案为:6+2($\sqrt{6}+\sqrt{2}+\sqrt{3}$)
点评 本题考查了解三角形在实际生活中的运用,学会利用角度和边长的关系建立等式,灵活运用正弦定理.属于中档题.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π-1}{4}$ | B. | $\frac{π-1}{2}$ | C. | $\frac{π-2}{4}$ | D. | $\frac{π-2}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若xy=0,则x=0”的否命题为“若xy≠0,则x≠0” | |
| B. | 命题“?x∈R,x2-x-1≤0”的否定是“$?{x_0}∈{R},{x_0}^2-{x_0}-1>0$” | |
| C. | 若p,q均为假命题,则p∧q为假命题 | |
| D. | 命题“?x∈[1,2],x2-a≤0”为真命题的一个充分不必要条件是a≥4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com