
分析 由题意,圆看成是圆外一点(原点0)向圆作两条交线.根据割线定理即可得到答案.
解答 解:由题意:圆C过点A(2,0),B(4,0),相当于圆与直线AB相交,∴|OA|=2,|OB|=4
直线l过原点O,与圆C交于P,Q两点,即为圆外一点(原点0)向圆作两条割线AB与PQ.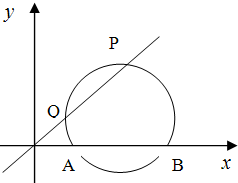
∵O,P,Q三点在一条直线上,夹角为0,
cos0=$\frac{\overrightarrow{OP}•\overrightarrow{OQ}}{|OP|•|OQ|}$,
∴$\overrightarrow{OP}$•$\overrightarrow{OQ}$=|OQ|•|OP|,
由圆的割线定理知:|OQ|•|OP|=|OA|•|OB|=8,
所以:$\overrightarrow{OP}$•$\overrightarrow{OQ}$=8,
故答案为:8.
点评 本题主要考查直线和圆的割线长度关系,利用割线定理求解.属于基础题.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(Χ2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
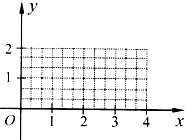 已知函数$f(x)=\left\{\begin{array}{l}{\sqrt{2}^x},x∈[0,2]\\ \frac{4}{x},x∈(2,4].\end{array}\right.$
已知函数$f(x)=\left\{\begin{array}{l}{\sqrt{2}^x},x∈[0,2]\\ \frac{4}{x},x∈(2,4].\end{array}\right.$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com