Question

3．已知正方形ABCD的边长为2，E、F、G、H分别是边AB、BC、CD、DA的中点．
（1）在正方形ABCD内部随机取一点P，求满足|PE|＜1的概率；
（2）从A、B、C、D、E、F、G、H这八个点中，随机选取两个点，记这两个点之间的距离的平方为ξ，求随机变量ξ的分布列与数学期望Eξ．

Answer 1

分析 （1）这是一个几何概型，点构成的区域是正方形ABCD的内部，满足|PE|＜1的点P构成的平面区域是以E为圆心，1为半径的圆的内部与正方形ABCD内部的公共部分，利用几何概率计算公式即可得出．
（2）从A、B、C、D、E、F、G、H这八个点中，任意选取两个点，共可构成${∁}_{8}^{2}$=28条不同的线段，其中长度为1的线段有8条，长度为$\sqrt{2}$的线段有4条，长度为2的线段有6条，长度为$\sqrt{5}$的线段有8条，长度为2$\sqrt{2}$的线段有2条．
可得：ξ所有可能的取值为1，2，4，5，8．利用古典概率计算公式即可得出概率、分布列及其数学期望．

解答 解：（1）这是一个几何概型，点构成的区域是正方形ABCD的内部，S_{正方形ABCD}=4．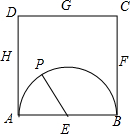
满足|PE|＜1的点P构成的平面区域是以E为圆心，1为半径的圆的内部与正方形ABCD内部的公共部分，其面积$S=\frac{π}{2}$．
∴满足|PE|＜1的概率为$\frac{π}{8}$．
（2）从A、B、C、D、E、F、G、H这八个点中，任意选取两个点，共可构成${∁}_{8}^{2}$=28条不同的线段，其中长度为1的线段有8条，长度为$\sqrt{2}$的线段有4条，长度为2的线段有6条，长度为$\sqrt{5}$的线段有8条，长度为2$\sqrt{2}$的线段有2条．
∴ξ所有可能的取值为1，2，4，5，8．
且P（ξ=1）$\frac{8}{28}$=$\frac{2}{7}$，P（ξ=2）=$\frac{4}{28}$=$\frac{1}{7}$，P（ξ=4）$\frac{6}{28}$=$\frac{3}{14}$，P（ξ=5）=$\frac{8}{28}$=$\frac{2}{7}$，P（ξ=8）=$\frac{2}{28}$=$\frac{1}{14}$．
∴随机变量ξ的分布列为：

ξ	1	2	4	5	8
P	$\frac{2}{7}$	$\frac{1}{7}$	$\frac{3}{14}$	$\frac{2}{7}$	$\frac{1}{14}$

随机变量ξ的数学期望为E（ξ）=$1×\frac{2}{7}$+2×$\frac{1}{7}$+4×$\frac{3}{14}$+5×$\frac{2}{7}$+8×$\frac{1}{14}$=$\frac{24}{7}$．

点评 本题考查了几何概型、古典概率计算公式、离散性随机变量的分布列及其数学期望计算公式，考查了推理能力与计算能力，属于中档题．