
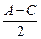 ,f(x)=cosB(
,f(x)=cosB(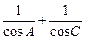 ).
).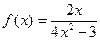 ,定义域为(
,定义域为( ,
, )∪(
)∪( ,1] (2) f(x)在(
,1] (2) f(x)在(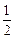 ,
,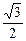 )和(
)和(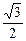 ,1
,1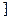 上都是减函数,(3) f(x)的值域为(-∞,-
上都是减函数,(3) f(x)的值域为(-∞,-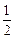 )∪[2,+∞
)∪[2,+∞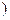
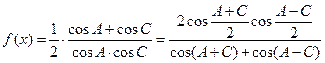
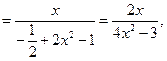
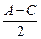 |<60°,∴x=cos
|<60°,∴x=cos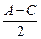 ∈(
∈( ,1
,1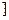
 ,∴定义域为(
,∴定义域为( ,
, )∪(
)∪( ,1].
,1]. 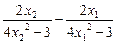 =
=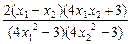 ,
,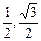 ),则4x12-3<0,4x22-3<0,4x1x2+3>0,x1-x2<0,∴f(x2)-f(x1)<0
),则4x12-3<0,4x22-3<0,4x1x2+3>0,x1-x2<0,∴f(x2)-f(x1)<0 ,1],则4x12-3>0.
,1],则4x12-3>0. ,
, )和(
)和( ,1
,1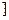 上都是减函数.
上都是减函数. )=-
)=- 或f(x)≥f(1)=2.
或f(x)≥f(1)=2. )∪[2,+∞
)∪[2,+∞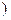 .
.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
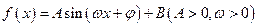 的一系列对应值如下表:
的一系列对应值如下表: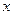 | 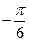 | 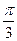 | 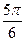 | 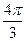 | 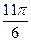 | 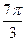 | 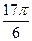 |
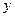 | 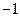 | 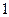 | 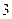 | 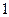 | 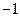 | 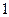 | 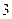 |
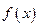 的一个解析式;
的一个解析式;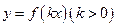 周期为
周期为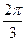 ,当
,当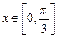 时,方程
时,方程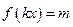 恰有两个不同的解,求实数
恰有两个不同的解,求实数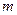 的取值范围;
的取值范围;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com