Question

【题目】如图，△ABC和△BCD所在平面互相垂直，且AB=BC=BD=2．∠ABC=∠DBC=120°，E、F分别为AC、DC的中点．

（1）求证：EF⊥BC；
（2）求二面角E﹣BF﹣C的正弦值．

Answer 1

【答案】
（1）证明：由题意，以B为坐标原点，在平面DBC内过B作垂直BC的直线为x轴，BC所在直线为y轴，在平面ABC内过B作垂直BC的直线为z轴，建立如图所示空间直角坐标系，易得B（0，0，0），A（0，﹣1， ），D（ ，﹣1，0），C（0，2，0），因而E（0， ， ），F（ ， ，0），所以 =（ ，0，﹣ ）， =（0，2，0），因此 =0，所以EF⊥BC．
（2）解：在图中，设平面BFC的一个法向量 =（0，0，1），平面BEF的法向量 =（x，y，z），又 =（ ， ，0）， =（0， ， ），

由 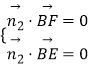得其中一个 =（1，﹣ ，1），

设二面角E﹣BF﹣C的大小为θ，由题意知θ为锐角，则

cosθ=|cos＜ ， ＞|=| |= ，

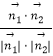因此sinθ= = ，即所求二面角正弦值为 ．

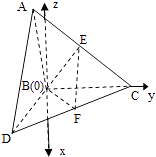
【解析】（1）以B为坐标原点，在平面DBC内过B作垂直BC的直线为x轴，BC所在直线为y轴，在平面ABC内过B作垂直BC的直线为z轴，建立如图所示空间直角坐标系，得到E、F、B、C点的坐标，易求得此 =0，所以EF⊥BC；（2）设平面BFC的一个法向量 =（0，0，1），平面BEF的法向量 =（x，y，z），依题意，可求得一个 =（1，﹣ ，1），设二面角E﹣BF﹣C的大小为θ，可求得sinθ的值．
【考点精析】根据题目的已知条件，利用直线与平面垂直的性质的相关知识可以得到问题的答案，需要掌握垂直于同一个平面的两条直线平行．