
分析 (1)由已知得(an-2n)+(an-1-2(n-1))=0,记cn=an-2n,则cn+cn-1=0,c1=0,由此能求出数列{an}的通项公式;
(2)由b1+3b2+7b3+…+(2n-1)bn=an,得b1+3b2+7b3+…+(2n-1-1)bn-1=an-1,从而得bn=$\frac{2}{{2}^{n}-1}$≤$\frac{3}{{2}^{n}}$,由此能证明Sn<$\frac{7}{2}$.
解答 解:(1)∵数列{an}满足a1=2,an+an+1=4n-2(n≥2,n∈N*),
∴(an-2n)+(an-1-2(n-1))=0,
记cn=an-2n,则cn+cn-1=0,c1=0,
∴cn=0,
∴an=2n.
证明:(2)∵数列{bn}满足b1+3b2+7b3+…+(2n-1)bn=an(n≥1,n∈N*),
∴b1+3b2+7b3+…+(2n-1-1)bn-1=an-1,(n≥2),
∴(2n-1)bn=an-an-1=2,
解得bn=$\frac{2}{{2}^{n}-1}$≤$\frac{3}{{2}^{n}}$,
∴Sn=b1+b2+…+bn
≤2+$\frac{3}{{2}^{2}}+\frac{3}{{2}^{3}}+…+\frac{3}{{2}^{n}}$
=2+3×$\frac{\frac{1}{{2}^{2}}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$
=$\frac{7}{2}-\frac{3}{{2}^{n}}$$<\frac{7}{2}$.
∴Sn<$\frac{7}{2}$.
点评 本题考查数列的通项公式的求法,考查不等式的证明,是中档题,解题时要认真审题,注意数列性质的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AP=1,AD=2,E为线段PD上一点,记$\frac{PE}{PD}$=λ. 当λ=$\frac{1}{2}$时,二面角D-AE-C的平面角的余弦值为$\frac{2}{3}$.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AP=1,AD=2,E为线段PD上一点,记$\frac{PE}{PD}$=λ. 当λ=$\frac{1}{2}$时,二面角D-AE-C的平面角的余弦值为$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
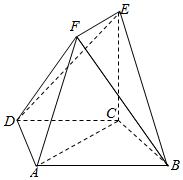 如图,四边形ABCD是等腰梯形,AB∥CD,∠ABC=60°,AB=2CB=4,在梯形ACEF中,EF∥AC,且AC=2EF,EC⊥平面ABCD.
如图,四边形ABCD是等腰梯形,AB∥CD,∠ABC=60°,AB=2CB=4,在梯形ACEF中,EF∥AC,且AC=2EF,EC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com