
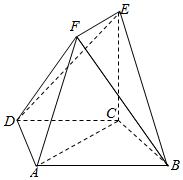
 如图,四边形ABCD是等腰梯形,AB∥CD,∠ABC=60°,AB=2CB=4,在梯形ACEF中,EF∥AC,且AC=2EF,EC⊥平面ABCD.
如图,四边形ABCD是等腰梯形,AB∥CD,∠ABC=60°,AB=2CB=4,在梯形ACEF中,EF∥AC,且AC=2EF,EC⊥平面ABCD.分析 (1)由余弦定理求出AC,得出AC⊥BC,又AC⊥CE得出AC⊥平面BCE,于是EF⊥平面BCE,故而平面BEF⊥平面BCE;
(2)以C为原点建立坐标系,设CE=h,求出平面ADF和平面ACF的法向量$\overrightarrow{n}$,$\overrightarrow{CB}$,令|cos<$\overrightarrow{n},\overrightarrow{CB}$>|=$\frac{\sqrt{2}}{2}$解出h,于是几何体ABCDEF的体积V=VD-ACEF+VB-ACEF.
解答  证明:(1)∵AB=4,BC=2,∠ABC=60°,∴AC=$\sqrt{A{B}^{2}+B{C}^{2}-2AB•BC•cos60°}$=2$\sqrt{3}$.
证明:(1)∵AB=4,BC=2,∠ABC=60°,∴AC=$\sqrt{A{B}^{2}+B{C}^{2}-2AB•BC•cos60°}$=2$\sqrt{3}$.
∴AC2+BC2=AB2,∴AC⊥BC.
∵CE⊥平面ABCD,AC?平面ABCD,∴CE⊥AC,又CE?平面BCE,BC?平面BCE,DE∩BC=C,
∴AC⊥平面BCE,
∵AC∥EF,∴EF⊥平面BCE,
又EF?平面BEF,
∴平面BEF⊥平面BCE.
(2)以C为原点,以CA,CB,CE为坐标轴建立空间直角坐标系如图所示:
设CE=h,则C(0,0,0),A(2$\sqrt{3}$,0,0),F($\sqrt{3}$,0,h),D($\sqrt{3}$,-1,0),B(0,2,0).
∴$\overrightarrow{AD}$=(-$\sqrt{3}$,-1,0),$\overrightarrow{AF}$=(-$\sqrt{3}$,0,h),
设平面ADF的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AD}=0}\\{\overrightarrow{n}•\overrightarrow{AF}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{-\sqrt{3}x-y=0}\\{-\sqrt{3}x+hz=0}\end{array}\right.$,令z=$\sqrt{3}$得$\overrightarrow{n}$=(h,-$\sqrt{3}$h,$\sqrt{3}$).
∵BC⊥平面ACEF,∴$\overrightarrow{CB}$=(0,2,0)为平面ACF的一个法向量,
∴cos<$\overrightarrow{n},\overrightarrow{CB}$>=$\frac{\overrightarrow{n}•\overrightarrow{CB}}{|\overrightarrow{n}||\overrightarrow{CB}|}$=$\frac{-2\sqrt{3}h}{2•\sqrt{4{h}^{2}+3}}$=-$\frac{\sqrt{3}h}{\sqrt{4{h}^{2}+3}}$.
∴$\frac{\sqrt{3}h}{\sqrt{4{h}^{2}+3}}$=cos45°=$\frac{\sqrt{2}}{2}$,
解得h=$\frac{\sqrt{6}}{2}$.即CE=$\frac{\sqrt{6}}{2}$.
∴VD-ACEF=$\frac{1}{3}{S}_{梯形ACEF}•|{y}_{D}|$=$\frac{1}{3}×\frac{1}{2}×(\sqrt{3}+2\sqrt{3})×\frac{\sqrt{6}}{2}×1$=$\frac{3\sqrt{2}}{4}$.
VB-ACEF=$\frac{1}{3}{S}_{梯形ACEF}•BC$=$\frac{1}{3}×\frac{1}{2}×(\sqrt{3}+2\sqrt{3})×\frac{\sqrt{6}}{2}×2$=$\frac{3\sqrt{2}}{2}$.
∴几何体ABCDEF的体积V=VD-ACEF+VB-ACEF=$\frac{3\sqrt{2}}{4}+\frac{3\sqrt{2}}{2}$=$\frac{9\sqrt{2}}{4}$.
点评 本题考查了面面垂直的判定,空间向量与二面角的计算,棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AD}$=-$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=-$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com