Question

（12分）如图，四边形ABCD是矩形，PA⊥平面ABCD，其中AB=3，PA=4，

若在线段PD上存在点E使得BE⊥CE，求线段AD的取值范围，并求当线段PD上有且只

有一个点E使得BE⊥CE时，二面角E—BC—A正切值的大小。

 

Answer 1

【答案】

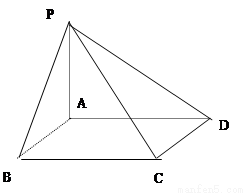
若以BC为直径的球面与线段PD有交点E，由于点E与BC确定的平面与球的截

面是一个大圆，则必有BE⊥CE，因此问题转化为以BC为直径的球与线段PD有交点。

设BC的中点为O（即球心），再取AD的中点M，易知OM⊥平面PAD，作ME⊥PD交PD于点E，连结OE，则OE⊥PD，所以OE即为点O到直线PD的距离，又因为OD＞OC，OP＞OA＞OB，点P，D在球O外，所以要使以BC为直径的球与线段PD有交点，只要使OE≤OC（设OC=OB=R）即可。

由于△DEM∽△DAP，可求得ME=  ，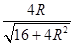

 

所以OE²=9+ 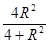  令OE²≤R²，即9+ 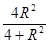≤R² ，解之得R≥2；

 

所以AD=2R≥4，所以AD的取值范围[ 4，+∞，

当且仅当AD= 4时，点E在线段PD上惟一存在，此时易求得二面角E—BC—A的平面角正切值为。

 

【解析】略