
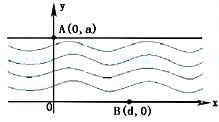
 如图,在直线y=0和y=a(a>0)之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往.家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读.每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d,0)处的学校.已知船速为υ0(υ0>0),车速为2υ0(水流速度忽略不计).
如图,在直线y=0和y=a(a>0)之间表示的是一条河流,河流的一侧河岸(x轴)是一条公路,且公路随时随处都有公交车来往.家住A(0,a)的某学生在位于公路上B(d,0)(d>0)处的学校就读.每天早晨该学生都要从家出发,可以先乘船渡河到达公路上某一点,再乘公交车去学校,或者直接乘船渡河到达公路上B(d,0)处的学校.已知船速为υ0(υ0>0),车速为2υ0(水流速度忽略不计).| a | 2 |
| ||
| υ0 |
| d-x |
| 2υ0 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| ||
| υ0 |
| d-x |
| 2υ0 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||||||
| υ0 |
d-
| ||||
| 2υ0 |
| ||
| 2 |
| a |
| υ0 |
| ||
| 2 |
| a |
| υ0 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| ||||
| υ0 |
| ||
| 2υ0 |
| a |
| 2 |
| ||
| 2υ0 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 (2011•自贡三模)给出下列5个命题:
(2011•自贡三模)给出下列5个命题:| 1 |
| 5 |
| 5π |
| 4 |
| 1 |
| 1-tanα |
| 2tanα |
| e-x+3 | ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
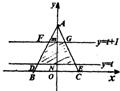 如图,在坐标平面内△ABC的顶点A(0,2),B(-1,0),C(1,0),有一个随t变化的带形区域,其边界为直线y=t和y=t+1,设这个带形区域覆盖△ABC的面积为S,试求以t为自变量的函数S的解析式,并画出这个函数的图象.
如图,在坐标平面内△ABC的顶点A(0,2),B(-1,0),C(1,0),有一个随t变化的带形区域,其边界为直线y=t和y=t+1,设这个带形区域覆盖△ABC的面积为S,试求以t为自变量的函数S的解析式,并画出这个函数的图象.查看答案和解析>>
科目:高中数学 来源:2009-2010学年河南省安阳一中高二(下)期中数学试卷(解析版) 题型:解答题
 ,求该学生早晨上学时,从家出发到达学校所用的最短时间.
,求该学生早晨上学时,从家出发到达学校所用的最短时间.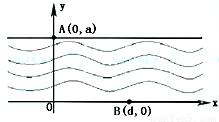
查看答案和解析>>
科目:高中数学 来源:2009-2010学年广东省湛江一中高二(下)模块数学试卷(选修2-2)(理科)(解析版) 题型:解答题
 ,求该学生早晨上学时,从家出发到达学校所用的最短时间.
,求该学生早晨上学时,从家出发到达学校所用的最短时间.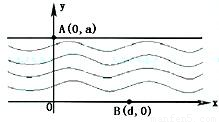
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com