解:(1)证明:∵对任意的x、y∈R,都有f(x+y)=f(x)+f(y),
,f(0)=f(0)+f(0)=2f(0),
∴f(0)=0.
令y=-x得,f(x-x)=f(x)+f(-x)=f(0)=0,
即f(-x)=-f(x),
∴函数f(x)为奇函数.
(2)f(x)在R上单调递减.
证明:设x
1<x
2,
则f(x
1)-f(x
2)=f(x
1)-f[(x
2-x
1)+x
1]=f(x
1)-[f(x
2-x
1)+f(x
1)]=-f[(x
2-x
1),
因为当x>0时,f(x)<0,且x
2-x
1>0,所以f[(x
2-x
1)<0,
所以f(x
1)-f(x
2)>0,即f(x
1)>f(x
2).
所以函数f(x)为R上的减函数.
由f(x+y)=f(x)+f(y)及f(-1)=2得,f(-2)=f(-1)+f(-1)=2f(-1)=4,
f(4)=f(2)+f(2)=2f(2),因为f(x)为奇函数,所以f(-2)=-f(2)=4,f(2)=-4,所以f(4)=-8.
又函数f(x)在区间[-2,4]上单调递减,所以f(4)≤f(x)≤f(-2),即-8≤f(x)≤4.
故函数f(x)在区间[-2,4]上的值域为[-8,4].
(3)因为函数f(x)在R上是奇函数,且单调递减,
所以不等式f(t
2-2kt)+f(2t
2-1)<0?f(t
2-2kt)<-f(2t
2-1)=f(1-2t
2)?t
2-2kt>1-2t
2,
所以对任意t∈[1,3],不等式f(t
2-2kt)+f(2t
2-1)<0恒成立,
等价于t
2-2kt>1-2t
2恒成立,即t∈[1,3]时2k<3t-

恒成立,
而易知3t-

在∈[1,3]上单调递增,所以
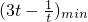
=3-1=2,
所以有2k<2,解得k<1.
所以实数k的取值范围为(-∞,1).
分析:(1)令x=y=0可得f(0)=0,令y=-x及奇函数的定义即得证;
(2)设x
1<x
2,则f(x
1)-f(x
2)=f(x
1)-f[(x
2-x
1)+x
1]=f(x
1)-[f(x
2-x
1)+f(x
1)]=-f[(x
2-x
1),根据已知可比较f(x
1)与f(x
2)的大小,从而可知其单调性;由函数的单调性及已知可求出f(-2),f(4),即函数f(x)在区间[-2,4]上的最值,由此可得其值域;
(3)利用函数f(x)的单调性、奇偶性,可把不等式f(t
2-2kt)+f(2t
2-1)<0中的符号“f”去掉,分离出参数k后转化为函数的最值问题即可求得.
点评:本题考查抽象函数的单调性、奇偶性及其应用,考查学生分析问题解决问题的能力,具有一定的综合性.

 恒成立,
恒成立, 在∈[1,3]上单调递增,所以
在∈[1,3]上单调递增,所以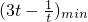 =3-1=2,
=3-1=2,

 活力课时同步练习册系列答案
活力课时同步练习册系列答案