
| A. | (-∞,0) | B. | [0,1) | C. | (-∞,1) | D. | [0,+∞) |
分析 由题知f(x)为分段函数,当x<0时,由f(x)=f(x+1)可知f(x)为周期函数;当x大于等于0时函数为增函数,而方程f(x)=-x+a有且只有两个不相等的实数根即f(x)与y=-x+a由两个交点,在同一坐标系中画出函数f(x)的图象与函数y=-x+a的图象,利用数形结合,易求出满足条件实数a的取值范围.
解答 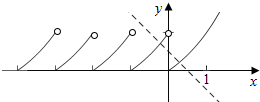 解:函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1(x≥0)}\\{f(x+1)(x<0)}\end{array}\right.$的图象如图所示,
解:函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-1(x≥0)}\\{f(x+1)(x<0)}\end{array}\right.$的图象如图所示,
作出直线l:y=a-x,向左平移直线l观察可得函数y=f(x)
的图象与函数y=-x+a的图象有两个交点,
即方程f(x)=-x+a有且只有两个不相等的实数根,
即有a<1,
故选:C.
点评 本题考查学生综合运用函数和方程的能力,以及让学生掌握数形结合的数学思想.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{8\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
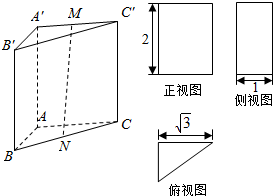 已知一个三棱柱ABC-A′B′C′的三视图由一个直角三角形和两个矩形组成,如图若M,N分别是A′C′,BC的中点.
已知一个三棱柱ABC-A′B′C′的三视图由一个直角三角形和两个矩形组成,如图若M,N分别是A′C′,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 两条直线平行,同旁内角互补,如果∠A和∠B是两条平行直线的同旁内角,则∠A+∠B=180° | |
| B. | 由平面三角形的性质,推测空间四面体的性质 | |
| C. | 某校高三共有10个班,1班有51人,2班有53人,三班有52人,由此推测各班都超过50人 | |
| D. | 在数列{an}中,a1=1,an=$\frac{1}{2}$(an-1+$\frac{1}{{a}_{n-1}}$)(n≥2),计算a2、a3,a4,由此猜测通项an |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com