练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如下图，等边△ABC的边长为4，D为BC中点，沿AD把△ADC折叠到△ADC′处，使二面角BADC′?为60°，则折叠后点A到直线BC′的距离为_________;二面角ABC′D的正切值为__________.

    答案:  2

    解析:(1)取BC′中点E，连结AE、DE，则AE即为A到BC′的距离.

    ∵△ABC为等边三角形，边长为4，

    故AD=.

    ∵BD⊥AD，DC′⊥AD，则∠BDC′即为二面角BADC′的平面角.

    ∴∠BDC′=60°，BD=DC′=2，则DE=.

    又∵AD⊥面BDE，则AD⊥DE，

    ∴.

    (2)DE⊥BC′，AE⊥BC′，则∠AED即为二面角ABC′D的平面角.

    ∴tan∠AED==2,即二面角ABC′D的正切值为2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：数学教研室 题型：044

    如下图，在边长为l的等边△ABC中，圆为△ABC的内切圆．圆与圆外切，且与AB、BC相切，…，圆与圆外切，且与AB、BC相切，如此无限继续下去，记圆的面积为（n∈N*）．

    （Ⅰ）证明{}是等比数列；（Ⅱ）求的值．

    查看答案和解析>>

    科目：高中数学 来源：导学大课堂必修二数学苏教版 苏教版 题型：013

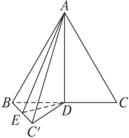
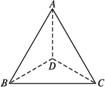
    如下图，在边长为a的等边三角形ABC中，AD⊥BC于D，沿AD折成二面角B－AD－C后，使BC＝，这时二面角B－AD－C的大小为

    [　　]

    A．30°

    B．45°

    C．60°

    D．90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如下图所示，在边长为l的等边△ABC中，⊙O1为△ABC中内切圆，⊙O2与⊙O1外切，且与AB、BC相切，…，⊙On+1与⊙On外切，且与AB、BC相切，如此无限继续下去，记⊙On的面积为an（n∈N*）.

    （1）证明{an}是等比数列；

    （2）求（a1+a2+…+an）的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

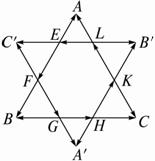
    如下图所示，△ABC和△A′B′C′是在各边的13处相交的两个全等正三角形．正△ABC的边长为a，图中列出了长度均为a3的若干个向量，则与相等的向量有多少个？与共线的向量有多少个？并写出这些向量．

    查看答案和解析>>

    同步练习册答案