考点:函数的最值及其几何意义
专题:导数的综合应用
分析:根据函数的性质,两个函数满足:增+增=增,减+减=减.所以先不忙于求函数的导数,先利用函数的性质单独讨论单调性,在参量a的范围缩小后再对函数求导;可从a=0、a-1=0、a与1-a两个中都为正、一正一负、一负一正、都为负入手.
解答:
解:直接从a 与1-a的符号分类:a<0时,1-a>0,故a与1-a不能同为负值,∴a与1-a的取值情况共有五类:
第一类:a=0;
第二类:1-a=0即a=1;
第三类:a<0时,1-a>0,即a<0;
第四类:a>0时,1-a<0,即a>1;
第五类:a>0时,1-a>0,即0<a<1;
(1)当a=0时,f(x)=
,∴f(x)在[
,2]递减;
(2)当a=1时,f(x)=x,∴f(x)在[
,2]递增;
(3)当a<0时,∵1-a>0,∵ax递减,
递减,∴f(x)在[
,2]递减;
此时,f(x)
min=
f(2)=2a+=
,即
fmin=f(2)=,
fmax=f()=;
(4)当a>1时,∵a>0时,1-a<0,∵ax递增,
递增,∴f(x)在[
,2]递增;
(5)当0<a<1时,∴a>0且1-a>0,
f′(x)=a-
=
==
∵x∈[
,2],∴x
2>0,
x+>0,又a>0,∴f′(x)的正负取决于
x-,
∴x∈(0,
)时,
x-<0,∴f′(x)<0,f(x)递减,
同理,x∈(
,+∞)时,f(x)递增,
∴当
≤
即
a≥时函数在[
,2]递增;当
≥2即
a≤时函数在[
,2]递减;
当
≤
≤2即
≤a≤时函数在[
,2]先减后增,∴
fmin=f()=
2,
再由
f()>f(2),即
(+)>(2a+),解得
a<,∴
fmax=f()=,
当
a≥时,f
max=f(2)=
;
∴综上五方面,①当
a≤时,函数在[
,2]递减,即
fmin=f(2)=,
fmax=f()=;
②当
a≥时,函数在[
,2]递增,此时,
fmin=f()=,f
max=f(2)=
;
③当
≤a≤时,函数在[
,2]先减后增,
fmin=f()=
2,
而最大值分两种情况:当
≤a≤时,
fmax=f()=;当
≤a≤时,时,f
max=f(2)=
.
点评:本题主要考查函数与导数的综合应用及分类讨论的数学思想.本题的难点在于函数表达式中参变量有两部分,处理的技巧是先不忙于求函数的导数,先利用函数的性质单独讨论单调性,在参量a的范围缩小后再对函数求导;其次,本题的另一难点在于,函数在区间先减后增时,函数的最大值在区间的端点取得,而大小还不一定,仍需要分类讨论.



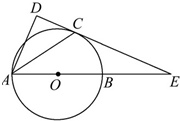 如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.