
如图,在四棱锥 中,
中, ⊥底面
⊥底面 ,底面
,底面
为正方形, ,
, ,
, 分别是
分别是 ,
, 的 中点.
的 中点.
(1)求证: 平面
平面 ;
;
(2)求证: ;
;
(3)若 是线段
是线段 上一动点,试确定
上一动点,试确定 点位置,
点位置,
使 平面
平面 ,并证明你的结论.
,并证明你的结论.
(1)详见解析;(2) 详见解析; (3)G是线段AD的中点.
解析试题分析:(1)证线面平行主要是利用线面平行的判定定理,其关键是找到面内直线与该直线平行,并要注明所证直线在面外的;2)证明线线垂直主要是转化为直线与平面垂直来证明的,而直线与平面垂直的证明又主要是通过证明直线与平面内的两条相交直线都垂直来实现的,再注意一直线垂直两平行线中的一条必垂直于另一条;(3)先由图形直观分析出点G应为线段AD的中点,再证明.
试题解析:(1)证明:
 ,
, 分别是
分别是 ,
, 的 中点,
的 中点,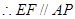 ,又
,又 ,
,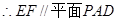 .
.
(2)因为四边形ABCD为正方形, 又
又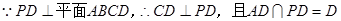 ,
,
(3)G是线段AD的中点时,GF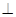 平面PCB.证明如下:
平面PCB.证明如下:
取BC的中点为H,连结DH,HF; PD=PC,
PD=PC,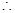 DH
DH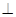 PC;又
PC;又 BC
BC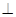 平面PDC,
平面PDC,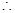 BC
BC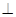 DH,
DH,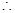 DH
DH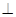 平面PCB.
平面PCB.
又 四边形DGFH为平行四边形,
四边形DGFH为平行四边形,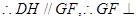 平面PCB.
平面PCB.
考点:1.线面平行;2.线面垂直.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:解答题
如图,ABCD是正方形,O是正方形的中心,PO 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。
求证:(1)PA∥平面BDE (4分)
(2)平面PAC 平面BDE(6分)
平面BDE(6分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图. 直三棱柱ABC —A1B1C1中,A1B1= A1C1,点D、E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.
求证:(1)平面ADE⊥平面BCC1B1
(2)直线A1F∥平面ADE.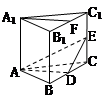
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(13分)(2011•广东)如图所示的几何体是将高为2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一半沿切面向右水平平移后得到的,A,A′,B,B′分别为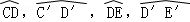 的中点,O1,O1′,O2,O2′分别为CD,C′D′,DE,D′E′的中点.
的中点,O1,O1′,O2,O2′分别为CD,C′D′,DE,D′E′的中点.
(1)证明:O1′,A′,O2,B四点共面;
(2)设G为A A′中点,延长A′O1′到H′,使得O1′H′=A′O1′.证明:BO2′⊥平面H′B′G
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com