
| A. |  | B. | 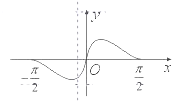 | ||
| C. | 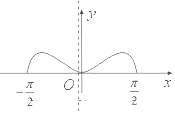 | D. | 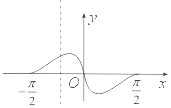 |
分析 利用函数的奇偶性排除选项,利用函数的特殊值对应点的位置排除选项得到结果.
解答 解:函数y=cosx•ln$\frac{{x}^{2}+2}{{2(x}^{2}+1)}$,x∈[-$\frac{π}{2}$,$\frac{π}{2}$]是偶函数,排除B,D,
当x=$\frac{π}{4}$时,y=$\frac{\sqrt{2}}{2}$•ln$\frac{\frac{{π}^{2}+8}{4}}{2(\frac{{π}^{2}+4}{4})}$=$\frac{\sqrt{2}}{2}$ln$\frac{{π}^{2}+8}{2{π}^{2}+8}$<0,排除C,
故选:A.
点评 本题考查函数的图象的判断,函数的奇偶性以及特殊值的判断是常用方法,考查计算能力.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 12 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P<N<M | B. | P<M<N | C. | M<P<N | D. | N<P<M |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{5}{2},-2]$ | B. | $[-\frac{5}{2},-2]$ | C. | [-2,0) | D. | [-2,0] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com