
【题目】(本小题满分12分)如图,曲线![]() 由上半椭圆
由上半椭圆![]() 和部分抛物线
和部分抛物线![]()
![]() 连接而成,
连接而成, ![]() 的公共点为
的公共点为![]() ,其中
,其中![]() 的离心率为
的离心率为![]() .
.
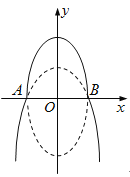
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)过点![]() 的直线
的直线![]() 与
与![]() 分别交于
分别交于![]() (均异于点
(均异于点![]() ),若
),若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ) ![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】试题分析:(1)由上半椭圆![]() 和部分抛物
和部分抛物![]() 公共点为
公共点为![]() ,得
,得![]() ,设
,设![]() 的半焦距为
的半焦距为![]() ,由
,由![]() 及
及![]() ,解得
,解得![]() ;
;
(2)由(1)知,上半椭圆![]() 的方程为
的方程为![]() ,
, ![]() ,易知,直线
,易知,直线![]() 与
与![]() 轴不重合也不垂直,故可设其方程为
轴不重合也不垂直,故可设其方程为![]() ,并代入
,并代入![]() 的方程中,整理得:
的方程中,整理得: ![]() ,
,
由韦达定理得![]() ,又
,又![]() ,得
,得![]() ,从而求得
,从而求得![]() ,继而得点
,继而得点![]() 的坐标为
的坐标为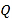 ,同理,由
,同理,由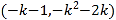 得点
得点![]() 的坐标为
的坐标为![]() ,最后由
,最后由![]() ,解得
,解得![]() ,经检验
,经检验![]() 符合题意,故直线
符合题意,故直线![]() 的方程为
的方程为![]() .
.
试题解析:(1)在![]() 方程中,令
方程中,令![]() ,得
,得![]()
在![]() 方程中,令
方程中,令![]() ,得
,得![]()
所以![]()
设![]() 的半焦距为
的半焦距为![]() ,由
,由![]() 及
及![]() ,解得
,解得![]()
所以![]() ,
, ![]()
(2)由(1)知,上半椭圆![]() 的方程为
的方程为![]() ,
, ![]()
易知,直线![]() 与
与![]() 轴不重合也不垂直,设其方程为
轴不重合也不垂直,设其方程为![]()
代入![]() 的方程中,整理得:
的方程中,整理得:
![]() (*)
(*)
设点![]() 的坐标
的坐标![]()
由韦达定理得![]()
又![]() ,得
,得![]() ,从而求得
,从而求得![]()
所以点![]() 的坐标为
的坐标为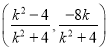
同理,由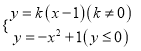 得点
得点![]() 的坐标为
的坐标为![]()
![]() ,
, ![]()
![]()
![]() ,即
,即![]()
![]() ,
, ![]() ,解得
,解得![]()
经检验, ![]() 符合题意,
符合题意,
故直线![]() 的方程为
的方程为![]()


科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
, ![]() ,外接球的球心为
,外接球的球心为![]() ,点
,点![]() 是侧棱
是侧棱![]() 上的一个动点.有下列判断:
上的一个动点.有下列判断:
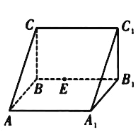
① 直线![]() 与直线
与直线![]() 是异面直线;②
是异面直线;②![]() 一定不垂直
一定不垂直![]() ;
;
③ 三棱锥![]() 的体积为定值; ④
的体积为定值; ④![]() 的最小值为
的最小值为![]() .
.
其中正确的序号序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
,左、右顶点分别为A,B,点M是椭圆C上异于A,B的一点,直线AM与y轴交于点P.
(Ⅰ)若点P在椭圆C的内部,求直线AM的斜率的取值范围;
(Ⅱ)设椭圆C的右焦点为F,点Q在y轴上,且∠PFQ=90°,求证:AQ∥BM.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差![]() ,
,![]() 和患感冒的小朋友人数(
和患感冒的小朋友人数(![]() /人)的数据如下:
/人)的数据如下:
温差 |
|
|
|
|
|
|
患感冒人数 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)请用相关系数加以说明是否可用线性回归模型拟合![]() 与
与的关系;
(Ⅱ)建立![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() ),预测当昼夜温差升高
),预测当昼夜温差升高![]() 时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
参考数据:![]() .参考公式:相关系数:
.参考公式:相关系数: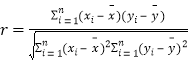 ,回归直线方程是
,回归直线方程是![]() ,
,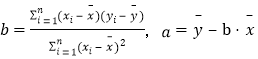 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,AD∥BC,BC=2AD,E,F分别为AD,BC的中点,AE=EF,![]() .将四边形ABFE沿EF折起,使平面ABFE⊥平面EFCD(如图2),G是BF的中点.
.将四边形ABFE沿EF折起,使平面ABFE⊥平面EFCD(如图2),G是BF的中点.
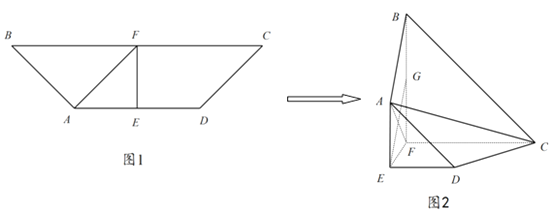
(1)证明:AC⊥EG;
(2)在线段BC上是否存在一点H,使得DH∥平面ABFE?若存在,求![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)求二面角D-AC-F的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对给定的d∈N*,记由数列构成的集合![]() .
.
(1)若数列{an}∈Ω(2),写出a3的所有可能取值;
(2)对于集合Ω(d),若d≥2.求证:存在整数k,使得对Ω(d)中的任意数列{an},整数k不是数列{an}中的项;
(3)已知数列{an},{bn}∈Ω(d),记{an},{bn}的前n项和分别为An,Bn.若|an+1|≤|bn+1|,求证:An≤Bn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程为ρ=4cosθ,以极点为原点,极轴为x轴正半轴建立平面直角坐标系,设直线l的参数方程为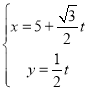 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程与直线l的普通方程;
(2)设曲线C与直线l相交于P,Q两点,以PQ为一条边作曲线C的内接矩形,求该矩形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com