
【题目】在正方体![]() 中,点
中,点![]() 平面
平面![]() ,点
,点![]() 是线段
是线段![]() 的中点,若
的中点,若![]() ,则当
,则当![]() 的面积取得最小值时,
的面积取得最小值时,![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据![]() 分析出点
分析出点![]() 在直线
在直线![]() 上,当
上,当![]() 的面积取得最小值时,线段
的面积取得最小值时,线段![]() 的长度为点
的长度为点![]() 到直线
到直线![]() 的距离,即可求得面积关系.
的距离,即可求得面积关系.
先证明一个结论P:若平面外的一条直线l在该平面内的射影垂直于面内的直线m,则l⊥m,
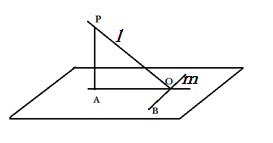
即:已知直线l在平面内的射影为直线OA,OA⊥OB,求证:l⊥OB.
证明:直线l在平面内的射影为直线OA,
不妨在直线l上取点P,使得PA⊥OB,OA⊥OB,OA,PA是平面PAO内两条相交直线,
所以OB⊥平面PAO,![]() 平面PAO,
平面PAO,
所以PO⊥OB,即l⊥OB.以上这就叫做三垂线定理.
如图所示,取![]() 的中点
的中点![]() ,
,
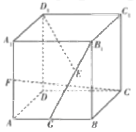
正方体中:![]() ,
,![]() 在平面
在平面![]() 内的射影为
内的射影为![]() ,
,
由三垂线定理可得:![]() ,
,
![]() 在平面
在平面![]() 内的射影为
内的射影为![]() ,
,![]()
由三垂线定理可得:![]() ,
,![]() 与
与![]() 是平面
是平面![]() 内两条相交直线,
内两条相交直线,
所以![]() 平面
平面![]() ,
,
∴当点![]() 在直线
在直线![]() 上时,
上时,![]() ,
,
设![]() ,则
,则![]() ,
,
当![]() 的面积取最小值时,
的面积取最小值时,
线段![]() 的长度为点
的长度为点![]() 到直线
到直线![]() 的距离,
的距离,
∴线段![]() 长度的最小值为
长度的最小值为![]() ,
,
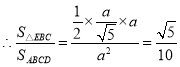 .
.
故选:D.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若![]() ,求函数
,求函数![]() 的零点;
的零点;
(2)若不存在相异实数![]() 、
、![]() ,使得
,使得![]() 成立.求实数
成立.求实数![]() 的取值范围;
的取值范围;
(3)若对任意实数![]() ,总存在实数
,总存在实数![]() 、
、![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
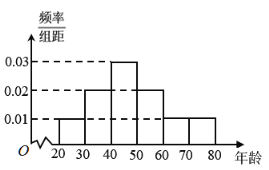
【题目】退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势.某机构为了了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在[20,80]内的600人进行调查,并按年龄层次绘制频率分布直方图,如图所示.若规定年龄分布在[60,80]内的人为“老年人”,将上述人口分布的频率视为该城市年龄段在[20,80]的人口分布的概率.从该城市年龄段在[20,80]内的市民中随机抽取3人,记抽到“老年人”的人数为![]() 则随机变量
则随机变量![]() 的数学期望为______.
的数学期望为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() 、
、![]() 的值;
的值;
(2)设函数![]() ,
,![]() (其中
(其中![]() 为自然对数的底数).
为自然对数的底数).
①当![]() 时,求
时,求![]() 的最大值;
的最大值;
②若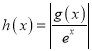 是单调递减函数,求实数
是单调递减函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行促销活动,有两个摸奖箱,![]() 箱内有一个“
箱内有一个“![]() ”号球,两个“
”号球,两个“![]() ”号球,三个“
”号球,三个“![]() ”号球、四个无号球,
”号球、四个无号球,![]() 箱内有五个“
箱内有五个“![]() ”号球,五个“
”号球,五个“![]() ”号球,每次摸奖后放回,每位顾客消费额满
”号球,每次摸奖后放回,每位顾客消费额满![]() 元有一次
元有一次![]() 箱内摸奖机会,消费额满
箱内摸奖机会,消费额满![]() 元有一次
元有一次![]() 箱内摸奖机会,摸得有数字的球则中奖,“
箱内摸奖机会,摸得有数字的球则中奖,“![]() ”号球奖
”号球奖![]() 元,“
元,“![]() ”号球奖
”号球奖![]() 元,“
元,“![]() ”号球奖
”号球奖![]() 元,摸得无号球则没有奖金。
元,摸得无号球则没有奖金。
(1)经统计,顾客消费额![]() 服从正态分布
服从正态分布![]() ,某天有
,某天有![]() 位顾客,请估计消费额
位顾客,请估计消费额![]() (单位:元)在区间
(单位:元)在区间![]() 内并中奖的人数.(结果四舍五入取整数)
内并中奖的人数.(结果四舍五入取整数)
附:若![]() ,则
,则![]() ,
,![]() .
.
(2)某三位顾客各有一次![]() 箱内摸奖机会,求其中中奖人数
箱内摸奖机会,求其中中奖人数![]() 的分布列.
的分布列.
(3)某顾客消费额为![]() 元,有两种摸奖方法,
元,有两种摸奖方法,
方法一:三次![]() 箱内摸奖机会;
箱内摸奖机会;
方法二:一次![]() 箱内摸奖机会.
箱内摸奖机会.
请问:这位顾客选哪一种方法所得奖金的期望值较大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的的参数方程为
的的参数方程为![]() (其中
(其中![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 经过点
经过点![]() .曲线
.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 作直线
作直线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点(
两点(![]() 在
在![]() 轴上方),求
轴上方),求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com