
【题目】已知函数![]()
(1)若![]() ,求函数
,求函数![]() 的零点;
的零点;
(2)若不存在相异实数![]() 、
、![]() ,使得
,使得![]() 成立.求实数
成立.求实数![]() 的取值范围;
的取值范围;
(3)若对任意实数![]() ,总存在实数
,总存在实数![]() 、
、![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的最大值.
的最大值.
【答案】(1)零点分别是:![]() 、
、![]() 、
、![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)解方程![]() 即可得出函数
即可得出函数![]() 的零点;
的零点;
(2)将函数![]() 的解析式表示为分段函数的形式,对实数
的解析式表示为分段函数的形式,对实数![]() 分
分![]() 、
、![]() 、
、![]() 三种情况讨论,分析函数
三种情况讨论,分析函数![]() 在区间
在区间![]() 上的单调性,结合题中结论可求得实数
上的单调性,结合题中结论可求得实数![]() 的取值范围;
的取值范围;
(3)由题意可得![]() ,对实数
,对实数![]() 分
分![]() 、
、![]() 、
、![]() 三种情况讨论,分析函数
三种情况讨论,分析函数![]() 在区间
在区间![]() 上的单调性,求得函数
上的单调性,求得函数![]() 在区间
在区间![]() 上的最大值和最小值,进而可得出
上的最大值和最小值,进而可得出![]() ,由此可求得实数
,由此可求得实数![]() 的最大值.
的最大值.
(1)当![]() 时,
时,![]() ,令
,令![]() ,可得
,可得![]() ,
,
所以,![]() 或
或![]() ,解得
,解得![]() 或
或![]() ,
,
所以,当![]() 时,函数
时,函数![]() 的零点分别为
的零点分别为![]() 、
、![]() 、
、![]() ;
;
(2)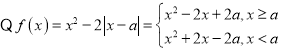 .
.
①当![]() 时,函数
时,函数![]() 在
在![]() 上递减,符合题意;
上递减,符合题意;
②当![]() 时,函数
时,函数![]() 在
在![]() 上递增,符合题意;
上递增,符合题意;
③当![]() 时,函数
时,函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,不符合题意.
上递减,不符合题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() ;
;
(3)由题意可得![]() .
.
①当![]() 时,函数
时,函数![]() 在
在![]() 上递减,
上递减,
则![]() ,
,![]() ,
,
![]() ;
;
②当![]() 时,函数
时,函数![]() 在
在![]() 上递增,
上递增,
![]() ,
,![]() ,
,
![]() ;
;
③当![]() 时,函数
时,函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
![]() ,
,![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
综上所述,![]() ,
,
因此,实数![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】齐王有上等,中等,下等马各一匹;田忌也有上等,中等,下等马各一匹.田忌的上等马优于齐王的中等马,劣于齐王的上等马;田忌的中等马优于齐王的下等马,劣于齐王的中等马;田忌的下等马劣于齐王的下等马.现从双方的马匹中随机各选一匹进行一场比赛,若有优势的马一定获胜,则齐王的马获胜的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,恰好又是双曲线
的焦点,恰好又是双曲线![]() 的右焦点,双曲线
的右焦点,双曲线![]() 过点
过点![]() ,且其离心率为
,且其离心率为![]() .
.
(1)求抛物线![]() 和双曲线
和双曲线![]() 的标准方程;
的标准方程;
(2)已知直线![]() 过点
过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() ,
,![]() 两点,以
两点,以![]() 为直径作圆
为直径作圆![]() ,设圆
,设圆![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】常州别称龙城,是一座有着3200多年历史的文化古城.常州既有春秋淹城、天宁寺等名胜古迹,又有中华恐龙园、嬉戏谷等游乐景点,每年都有大量游客来常州参观旅游.为合理配置旅游资源,管理部门对首次来中华恐龙园游览的游客进行了问卷调查,据统计,其中![]() 的人计划只游览中华恐龙园,另外
的人计划只游览中华恐龙园,另外![]() 的人计划既游览中华恐龙园又参观天宁寺.每位游客若只游览中华恐龙园,得1分;若既游览中华恐龙园又参观天宁寺,得2分.假设每位首次来中华恐龙园游览的游客均按照计划进行,且是否参观天宁寺相互独立,视频率为概率.
的人计划既游览中华恐龙园又参观天宁寺.每位游客若只游览中华恐龙园,得1分;若既游览中华恐龙园又参观天宁寺,得2分.假设每位首次来中华恐龙园游览的游客均按照计划进行,且是否参观天宁寺相互独立,视频率为概率.
(1)有2名首次来中华恐龙园游览的游客是拼车到常州的,求“这2名游客都是既游览中华恐龙园又参观天宁寺”的概率;
(2)从首次来中华恐龙园游览的游客中随机抽取3人,记这3人的合计得分为X,求X的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)存在![]() ,对任意
,对任意![]() ,有不等式
,有不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(2)如果存在![]() 、
、![]() ,使得
,使得![]() 成立,求满足条件的最大整数
成立,求满足条件的最大整数![]() ;
;
(3)对任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P一ABCD中,AB=AD=2BC=2,BC∥AD,AB⊥AD,△PBD为正三角形.且PA=2![]() .
.
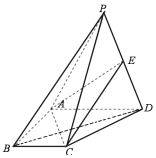
(1)证明:平面PAB⊥平面PBC;
(2)若点P到底面ABCD的距离为2,E是线段PD上一点,且PB∥平面ACE,求四面体A-CDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为 ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 与曲线
与曲线![]() 两交点所在直线的极坐标方程;
两交点所在直线的极坐标方程;
(2)若直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与曲线
,与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com