
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,恰好又是双曲线
的焦点,恰好又是双曲线![]() 的右焦点,双曲线
的右焦点,双曲线![]() 过点
过点![]() ,且其离心率为
,且其离心率为![]() .
.
(1)求抛物线![]() 和双曲线
和双曲线![]() 的标准方程;
的标准方程;
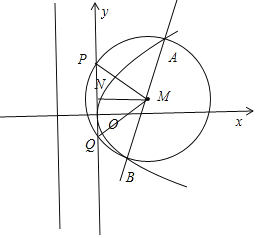
(2)已知直线![]() 过点
过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() ,
,![]() 两点,以
两点,以![]() 为直径作圆
为直径作圆![]() ,设圆
,设圆![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)抛物线E的标准方程为![]() ,双曲线C的标准方程为
,双曲线C的标准方程为![]() (2)
(2)![]()
【解析】
(1)由双曲线![]() 过点
过点![]() ,且其离心率为
,且其离心率为![]() .可得
.可得![]() ,
,![]() ,
,![]() ,联立解得:
,联立解得:![]() ,
,![]() ,
,![]() 即可得出双曲线
即可得出双曲线![]() 的标准方程.可得
的标准方程.可得![]() ,解得
,解得![]() .可得抛物线的标准方程.
.可得抛物线的标准方程.
(2)①当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为:
的方程为:![]() .此时
.此时![]() ,
,![]() .
.![]() 的方程为:
的方程为:![]() .可得
.可得![]() .
.
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为:
的方程为:![]() ,由题意可得:
,由题意可得:![]() .联立化为:
.联立化为:![]() .设
.设![]() ,
,![]() ,
,![]() ,
,![]() .利用根与系数的关系可得
.利用根与系数的关系可得![]() .设
.设![]() 的半径为
的半径为![]() ,
,![]() .过点
.过点![]() 作
作![]() ,垂足为
,垂足为![]() .在
.在![]() 中,
中,![]() ,可得
,可得![]() 范围,及其
范围,及其![]() 范围,即可得出结论.
范围,即可得出结论.
(1)由双曲线![]() 过点
过点![]() ,且其离心率为
,且其离心率为![]() .
.
![]()
![]() ,
,![]() ,
,![]() ,
,
联立解得:![]() ,
,![]() .
.
![]() 双曲线
双曲线![]() 的标准方程为:
的标准方程为:![]() .
.
由![]() ,可得
,可得![]() ,解得
,解得![]() .
.
![]() 抛物线的标准方程为:
抛物线的标准方程为:![]() .
.
(2)①当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为:
的方程为:![]() .此时
.此时![]() ,
,![]() .
.
![]() 的方程为:
的方程为:![]() .
.
可得![]() ,
,![]() .
.![]() .
.
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为:
的方程为:![]() ,
,
由题意可得:![]() .联立
.联立![]() ,化为:
,化为:![]() .
.
设![]() ,
,![]() ,
,![]() ,
,![]() .则
.则![]() ,
,![]() .
.
![]() ,
,
![]() .
.
设![]() 的半径为
的半径为![]() ,则
,则![]() .
.
过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
在![]() 中,
中,![]() .
.
![]() ,则
,则![]() .
.
综上可得:![]() 的最大值为
的最大值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
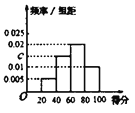
【题目】白塔中学为了解校园爱国卫生系列活动的成效,对全校学生进行了一次卫生意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
(1)求统计表、直方图中的a,b,c的值;
(2)用分层抽样的方法,从等级为“合格”和“不合格”的学生中抽取10人进行座谈.现再从这10人中任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有2名男生、3名女生,在下列不同条件下,求不同的排列方法总数.
(1)全体站成一排,甲不站排头也不站排尾;
(2)全体站成一排,女生必须站在一起;
(3)全体站成一排,男生互不相邻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在某市的一次学情检测中,学生的数学成绩X服从正态分布N(105,100),其中90分为及格线,120分为优秀线,下列说法正确的是( )
附:随机变量![]() 服从正态分布N(
服从正态分布N(![]() ,
,![]() ),则P(
),则P(![]() )=0.6826,P(
)=0.6826,P(![]() )=0.9544,P(
)=0.9544,P(![]() )=0.9974.
)=0.9974.
A.该市学生数学成绩的期望为105
B.该市学生数学成绩的标准差为100
C.该市学生数学成绩及格率超过0.99
D.该市学生数学成绩不及格的人数和优秀的人数大致相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若![]() ,求函数
,求函数![]() 的零点;
的零点;
(2)若不存在相异实数![]() 、
、![]() ,使得
,使得![]() 成立.求实数
成立.求实数![]() 的取值范围;
的取值范围;
(3)若对任意实数![]() ,总存在实数
,总存在实数![]() 、
、![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com