
【题目】已知在某市的一次学情检测中,学生的数学成绩X服从正态分布N(105,100),其中90分为及格线,120分为优秀线,下列说法正确的是( )
附:随机变量![]() 服从正态分布N(
服从正态分布N(![]() ,
,![]() ),则P(
),则P(![]() )=0.6826,P(
)=0.6826,P(![]() )=0.9544,P(
)=0.9544,P(![]() )=0.9974.
)=0.9974.
A.该市学生数学成绩的期望为105
B.该市学生数学成绩的标准差为100
C.该市学生数学成绩及格率超过0.99
D.该市学生数学成绩不及格的人数和优秀的人数大致相等
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】某农场更新技术培育了一批新型的“盆栽果树”,这种“盆栽果树”将一改陆地栽植果树只在秋季结果的特性,能够一年四季都有花、四季都结果.现为了了解果树的结果情况,从该批果树中随机抽取了容量为120的样本,测量这些果树的高度(单位:厘米),经统计将所有数据分组后得到如图所示的频率分布直方图.
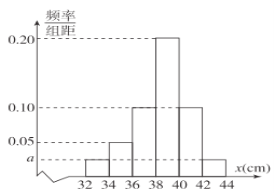
(1)求![]() ;
;
(2)已知所抽取的样本来自![]() 两个实验基地,规定高度不低于40厘米的果树为“优品盆栽”,
两个实验基地,规定高度不低于40厘米的果树为“优品盆栽”,
(i)请将图中列联表补充完整,并判断是否有![]() 的把握认为“优品盆栽”与
的把握认为“优品盆栽”与![]() 两个实验基地有关?
两个实验基地有关?
优品 | 非优品 | 合计 | |
| 60 | ||
| 20 | ||
合计 |
(ii)用样本数据来估计这批果树的生长情况,若从该农场培育的这批“盆栽果树”中随机抽取4棵,求其中“优品盆栽”的棵树![]() 的分布列和数学期望.
的分布列和数学期望.
附:
|
|
|
|
|
|
|
|
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,恰好又是双曲线
的焦点,恰好又是双曲线![]() 的右焦点,双曲线
的右焦点,双曲线![]() 过点
过点![]() ,且其离心率为
,且其离心率为![]() .
.
(1)求抛物线![]() 和双曲线
和双曲线![]() 的标准方程;
的标准方程;
(2)已知直线![]() 过点
过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() ,
,![]() 两点,以
两点,以![]() 为直径作圆
为直径作圆![]() ,设圆
,设圆![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的图象为C,如下结论中正确的是( )
的图象为C,如下结论中正确的是( )
①图象C关于直线![]() 对称;②函数
对称;②函数![]() 在区间
在区间![]() 内是增函数;
内是增函数;
③图象C关于点![]() 对称;④由
对称;④由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象C
个单位长度可以得到图象C
A.①③B.②③C.①②③D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】常州别称龙城,是一座有着3200多年历史的文化古城.常州既有春秋淹城、天宁寺等名胜古迹,又有中华恐龙园、嬉戏谷等游乐景点,每年都有大量游客来常州参观旅游.为合理配置旅游资源,管理部门对首次来中华恐龙园游览的游客进行了问卷调查,据统计,其中![]() 的人计划只游览中华恐龙园,另外
的人计划只游览中华恐龙园,另外![]() 的人计划既游览中华恐龙园又参观天宁寺.每位游客若只游览中华恐龙园,得1分;若既游览中华恐龙园又参观天宁寺,得2分.假设每位首次来中华恐龙园游览的游客均按照计划进行,且是否参观天宁寺相互独立,视频率为概率.
的人计划既游览中华恐龙园又参观天宁寺.每位游客若只游览中华恐龙园,得1分;若既游览中华恐龙园又参观天宁寺,得2分.假设每位首次来中华恐龙园游览的游客均按照计划进行,且是否参观天宁寺相互独立,视频率为概率.
(1)有2名首次来中华恐龙园游览的游客是拼车到常州的,求“这2名游客都是既游览中华恐龙园又参观天宁寺”的概率;
(2)从首次来中华恐龙园游览的游客中随机抽取3人,记这3人的合计得分为X,求X的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P一ABCD中,AB=AD=2BC=2,BC∥AD,AB⊥AD,△PBD为正三角形.且PA=2![]() .
.
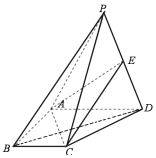
(1)证明:平面PAB⊥平面PBC;
(2)若点P到底面ABCD的距离为2,E是线段PD上一点,且PB∥平面ACE,求四面体A-CDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,直线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com