
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,直线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,求
两点,求![]() 的面积.
的面积.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且
,且![]() ,抛物线的通径与椭圆的右通径在同一直线上.
,抛物线的通径与椭圆的右通径在同一直线上.
(1)求椭圆与抛物线的标准方程;
(2)过抛物线焦点且倾斜角为![]() 的直线与椭圆交于
的直线与椭圆交于![]() 、
、![]() 两点,
两点,![]() 为椭圆的左焦点,求
为椭圆的左焦点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]()
![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,且当倾斜角为
两点,且当倾斜角为![]() 的直线
的直线![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() 时,有
时,有![]() .
.
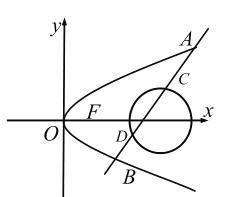
(1)求抛物线![]() 的方程;
的方程;
(2)已知圆![]() ,是否存在倾斜角不为
,是否存在倾斜角不为![]() 的直线
的直线![]() ,使得线段
,使得线段![]() 被圆
被圆![]() 截成三等分?若存在,求出直线
截成三等分?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了了解人们]对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15∽65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
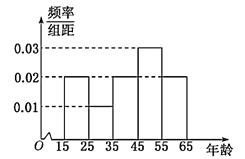
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率.
②记抽到45岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园根据部分同年龄段的100名女童的身高数据绘制了频率分布直方图,其中身高的变化范围是[96,106](单位:厘米),样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).
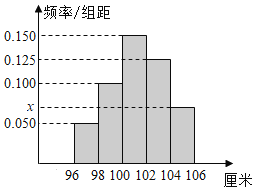
(1)求出![]() 的值,并求样本中女童的身高的众数和中位数,平均数;
的值,并求样本中女童的身高的众数和中位数,平均数;
(2)在身高在[100,102),[102,104),[104,106]的三组中,用分层抽样的方法抽取14名女童,则身高数据在[104,106]的女童中应抽取多少人数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为我国数学家赵爽![]() 约3世纪初
约3世纪初![]() 在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则
在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则![]() 区域涂色不相同的概率为
区域涂色不相同的概率为![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,且
,且![]() ,椭圆经过点
,椭圆经过点![]() .
.
(1)求椭圆的方程;
(2)直线![]() 过椭圆右顶点
过椭圆右顶点![]() ,交椭圆于另一点
,交椭圆于另一点![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .若
.若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com