已知x,y∈R,2x+3y=13,则x2+y2+1的最小值为________.
14
分析:解法1:利用解析几何的性质可知3x+y=10表示直线的方程,则x
2+y
2表示直线上的点到原点的距离,推断出原点到直线3x+y=10距离为直线的点到原点的最短距离,最后利用点到直线的距离求得问题的答案.
解法2:欲求x
2+y
2的最小值,根据它与条件的结构特点,考虑利用柯西不等式解决.
解答:解法1:根据解析几何的性质可知,2x+3y=13表示直线的方程,
则x
2+y
2表示直线上的点到原点的距离的平方,
由于原点到直线2x+3y=13距离为直线的点到原点的最短距离,
故x
2+y
2的最小值为(
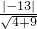
)
2=13,
则x
2+y
2+1的最小值为14;
解法2:因为2x+3y=13,
所以利用柯西不等式得
(x
2+y
2)(2
2+3
2)≥(2x+3y)
2,
即13(x
2+y
2)≥13
2,
即x
2+y
2≥13,
当且仅当
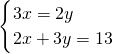
即
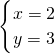
时取等号,
即x
2+y
2的最小值为13.
则x
2+y
2+1的最小值为14.
故答案为:14
点评:本题主要考查了点到直线的距离的应用,曲线方程与不等式的综合.考查了学生数形结合的思想的应用.要求学生尝试利用多种方法来解题,培养了学生一题多解的能力.

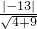 )2=13,
)2=13,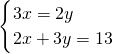 即
即 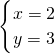 时取等号,
时取等号,

 计算高手系列答案
计算高手系列答案