
已知数列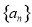 满足
满足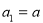 ,
,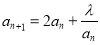 ,(
,(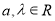 )
)
(1)若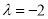 ,数列
,数列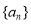 单调递增,求实数
单调递增,求实数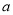 的取值范围;
的取值范围;
(2)若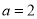 ,试写出
,试写出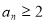 对任意
对任意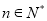 成立的充要条件,并证明你的结论.
成立的充要条件,并证明你的结论.
(1) ∪
∪ ;(2)充要条件为
;(2)充要条件为 .
.
【解析】
试题分析:本题主要考查数列的递推公式、数列的单调性、充要条件、数学归纳法等基础知识,考查学生的分析问题解决问题的能力、计算能力、逻辑推理能力.第一问,数列 单调递增
单调递增 ,将已知条件代入,得到
,将已知条件代入,得到 所满足条件,即
所满足条件,即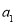 需要满足的条件,即得到a的取值范围,第二问,必要性:法一:由
需要满足的条件,即得到a的取值范围,第二问,必要性:法一:由 直接解出
直接解出 ,法二:利用已知的递推公式得到
,法二:利用已知的递推公式得到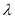 与
与 的关系,再利用配方法得到
的关系,再利用配方法得到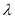 的最小值,充分性:用数学归纳法证明.
的最小值,充分性:用数学归纳法证明.
试题解析:(1)若 ,则
,则 ,
,
由 ,
,
得 或
或 ,所以只需
,所以只需 或
或 .
.
所以实数 的取值范围为
的取值范围为 ∪
∪ . 6分
. 6分
(2) 对任意
对任意 成立的充要条件为
成立的充要条件为 .必要性:由
.必要性:由 ,解出
,解出 ;
;
(另【解析】
假设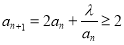 ,得
,得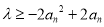 ,令
,令 ,
, ,可得:
,可得: ,即有
,即有 .) 8分
.) 8分
充分性:数学归纳法证明: 时,对一切
时,对一切 ,
, 成立.
成立.
证明:(1)显然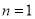 时,结论成立;
时,结论成立;
(2)假设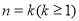 时结论成立,即
时结论成立,即 ,
,
当 时,
时,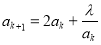 .
.
考察函数 ,
, ,
,
①若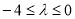 ,由
,由 ,知
,知 在区间
在区间 上单调递增.由假设
上单调递增.由假设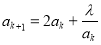
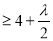
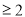 .
.
②若 ,对
,对 总有
总有 ,
,
则由假设得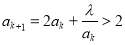 .
.
所以, 时,结论成立,
时,结论成立,
综上可知:当 时,对一切
时,对一切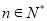 ,
, 成立.
成立.
故 对任意
对任意 成立的充要条件是
成立的充要条件是 .
.
考点:数列的递推公式、数列的单调性、充要条件、数学归纳法.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源:2013-2014学年山东省东营市高三4月统一质量检测考试理科数学试卷(解析版) 题型:选择题
函数 的部分图像如图所示,则
的部分图像如图所示,则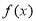 的解析式可以是( )
的解析式可以是( )

A. B.
B.
C.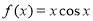 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省皖北协作区高三年级联考理科数学试卷(解析版) 题型:选择题
若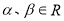 且
且 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省皖北协作区高三年级联考文科数学试卷(解析版) 题型:选择题
设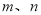 是不同的直线,
是不同的直线,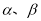 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
①若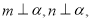 则
则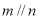
②若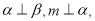 则
则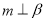
③若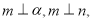 则
则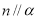
④若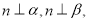 则
则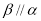
其中真命题的序号是( )
A、①③ B、①④ C、②③ D、②④
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省安庆市高三第二次模拟考试理科数学试卷(解析版) 题型:解答题
已知向量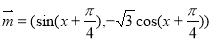 ,
, ,函数
,函数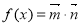 ,
, .
.
(1)求函数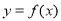 的图像的对称中心坐标;
的图像的对称中心坐标;
(2)将函数 图像向下平移
图像向下平移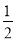 个单位,再向左平移
个单位,再向左平移 个单位得函数
个单位得函数 的图像,试写出
的图像,试写出 的解析式并作出它在
的解析式并作出它在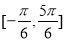 上的图像.
上的图像.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省安庆市高三第二次模拟考试文科数学试卷(解析版) 题型:填空题
甲、乙两位同学参加2014年的自主招生考试,下火车后两人共同提起一个行李包(如图所示).设他们所用的力分别为 ,行李包所受重力为
,行李包所受重力为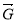 ,若
,若 ,则
,则 与
与 的夹角
的夹角 的大小为____________.
的大小为____________.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省合肥市高三第二次教学质量检测文科数学试卷(解析版) 题型:选择题
若全集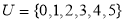 ,且
,且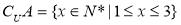 ,则集合
,则集合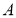 的真子集共有( )
的真子集共有( )
A.3个 B.4个 C.7个 D.8个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com