
| OP |
| 1 |
| 6 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 2 |
| OC |
| OP |
| 1 |
| 6 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 2 |
| OC |
| PA |
| PB |
| PC |
| 0 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
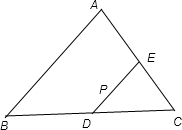 解:记△ABP、△BCP、△ACP的面积依次为S1、S2、S3.
解:记△ABP、△BCP、△ACP的面积依次为S1、S2、S3.| OP |
| 1 |
| 6 |
| OA |
| 1 |
| 3 |
| OB |
| 1 |
| 2 |
| OC |
| PA |
| PB |
| PC |
| 0 |
| PA |
| PB |
| PB |
| PC |
| BA |
| PD |
| PD |
| PA |
| PC |
| PB |
| PC |
| PE |
| PD |
| PE |
| 1 |
| 3 |
| BA |
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2S |
| l |
| 3V |
| S |
| ||
| 2 |
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、两条直线平行,同旁内角互补,如果∠A和∠B是两条平行直线的同旁内角,则∠A+∠B=180° |
| B、由平面向量的运算性质,推测空间向量的运算性质 |
| C、某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员 |
| D、一切偶数都能被2整除,2100是偶数,所以2100能被2整除 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com