新学期开始.哈六中接受6名师大学生到校实习.学校要把他们分到三个年级.每个年级2名.其中甲必须在高一年级.乙和丙均不能在高三年级.则不同的安排方法种数为( )A．18B．15C．12D．9 题目和参考答案——青夏教育精英家教网—

7．新学期开始，哈六中接受6名师大学生到校实习，学校要把他们分到三个年级，每个年级2名，其中甲必须在高一年级，乙和丙均不能在高三年级，则不同的安排方法种数为（　　）

A．

B．

C．

D．

分析本题要先安排乙和丙两人，其安排方法可以分为两类，一类是两之一在高一，一在高二，另一类是两者都在高二，在每一类中用分步原理计算种数即可．

解答解：若乙和丙两人有一人在高一，另一人在高二，则第一步安排高一有2种安排方法，第二步安排高二，从三人中选一人有三种方法，第二步余下两人去高三，一种方法；故此类中安排方法种数是2×3=6；
若乙和丙两人在高二，第一步安排高一，有三种安排方法，第二步安排高三，余下两人去高三，一种安排方法，故总的安排方法有3×1=3；
综上，总的安排方法种数有6+3=9种．
故选：D．

点评本题考查分步原理与分类原理的应用，求解本题关键是根据实际情况选择正确的分类标准与分步标准，把实际问题的结构理解清楚．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

17．定义复数的一种运算z₁*z₂=$\frac{|{z}_{1}|+|{z}_{2}|}{2}$ （等式右边为普通运算），若复数z=a+bi，$\overline{z}$为z的共轭复数，且正实数a，b满足a+b=3，则z*$\overline{z}$的最小值为（　　）

A．

$\frac{9}{2}$

B．

$\frac{3\sqrt{2}}{2}$

C．

$\frac{3}{2}$

D．

$\frac{9}{4}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

18．

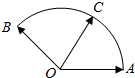给定两个长度为1的平面向量$\overrightarrow{OA}$和$\overrightarrow{OB}$，它们的夹角为120°．点C在以OA，OB为半径的圆弧上，∠AOC=30°如图所示，若$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$，其中x，y∈R，则x=$\frac{2\sqrt{3}}{3}$；y=$\frac{\sqrt{3}}{3}$．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

15．设0＜b＜a＜1，则下列不等式不成立的是（　　）

	A．	2^b＜2^a＜2		B．	$0＜{log_{\frac{1}{2}}}a＜{log_{\frac{1}{2}}}$b
	C．	ab＜b²＜1		D．	ab＜a²＜1

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

2．

设△ABC的内角A、B、C所对的边分别为a、b、c，$\frac{5（sinA-sinC）}{sin（A+C）}=\frac{5sinB-8sinC}{sinA+sinC}$，点P为△ABC内任意一点，点P到三边的距离之和为d．
（1）求sinA的值；
（2）若a=3，c=5，求边b的长；
（3）在（2）的条件下，建立如图平面直角坐标系xOy，求d的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

12．若函数f（x）=|a^x+x²-xlna-m|-3（a＞0且a≠1）有两个零点，则m的取值范围（　　）

A．

（-2，4）

B．

（-4，2）

C．

（-1，3）

D．

（-3，1）

查看答案和解析>>