
分析 (1)在所给的等式中,令x=0,可得常数项a0=1;令x=1可得a0+a1+a2+a3+…+a7=-1,从而求得a1+a2+a3+…+a7的值.
(2)在所给的等式中,分别令x=1、-1,得到2个等式,再把这2个等式相减,可得a1+a3+a5+…+a7的值.
(3)在(1+2x)7 中,令x=1,可得要求式子的值.
解答 解:(1)在${(1-2x)^7}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_7}{x^7}$中,令x=0,可得常数项a0=1.
在所给的等式中,令x=1可得a0+a1+a2+a3+…+a7=-1,
∴a1+a2+a3+…+a7=-2.
(2)在所给的等式知${(1-2x)^7}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_7}{x^7}$中,令x=1可得a0+a1+a2+a3+…+a7=-1①,
令x=-1可得得${a_0}-{a_1}+{a_2}-{a_3}+…-{a_7}={3^7}$②,
用①减去②再除以2可得a1+a3+a5+…+a7=-1094.
(3)在(1+2x)7 中,令x=1,可得$|{a_0}|+|{a_1}|+|{a_2}|+…+|{a_7}|={3^7}=2187$.
点评 本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (0,1) | C. | (-1,+∞) | D. | (0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一段图象如图所示,
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一段图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
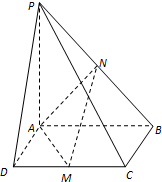 如图:已知四棱锥P-ABCD,底面是边长为6的正方形ABCD,PA=8,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM、AN、MN.
如图:已知四棱锥P-ABCD,底面是边长为6的正方形ABCD,PA=8,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM、AN、MN.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{19}{36}$ | B. | $\frac{11}{36}$ | C. | $\frac{7}{12}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com