
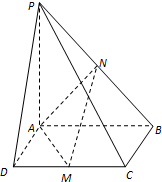
 如图:已知四棱锥P-ABCD,底面是边长为6的正方形ABCD,PA=8,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM、AN、MN.
如图:已知四棱锥P-ABCD,底面是边长为6的正方形ABCD,PA=8,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM、AN、MN.分析 (1)由题意,证明线线垂直,利用“三垂线定理或三垂线定理的逆定理”即可解决.
(2)异面直线所成角,首先要构造出这两条异面直线的平行线相交的角,即为异面直线所成角.由题意,分别取AB,PA中点E,F,连接CE,EF,CF,所以异面直线AM与PB所成角的大小即相交直线CF与EF所成角的大小.
解答 解:(1)分别取AB,PA中点E,F,连接CE,EF,CF,NE,ME.
∵E是AB中点,点N是PB的中点,
∴$E{N}_{=}^{∥}\frac{1}{2}AP$
∵PA⊥面ABCD,
∴NE⊥面ABCD,NE⊥AB.
又∵MN∥BC,∴MN⊥AB.
所以:AB⊥MN,
得证.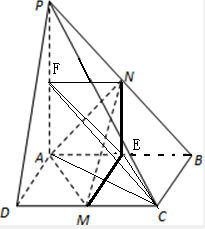
(2)∵E是AB中点,F是PA中点E,N是PB的中点,点M是CD的中点
∴AM${\;}_{=}^{∥}$CE,FE${\;}_{=}^{∥}\frac{1}{2}PB$.
所以:异面直线AM与PB所成角的大小即相交直线CF与EF所成角的大小
在△CEF中:EC=MA=$\sqrt{A{D}^{2}+D{M}^{2}}$=$3\sqrt{5}$,FE=$\frac{1}{2}PB=5$,FC=$\sqrt{A{F}^{2}+A{C}^{2}}=2\sqrt{22}$.
利用余弦定理:
cos∠FEC=$\frac{F{E}^{2}+E{C}^{2}-F{C}^{2}}{2EF•EC}=\frac{25+45-88}{2×3\sqrt{5}×5}=-\frac{3\sqrt{5}}{25}$
∵cos∠FEC<0,
∴∠FEC是钝角.
所以异面直线AM与PB所成角的大小为π-$arccos\frac{{3\sqrt{5}}}{25}$.
点评 本题考查了“三垂线定理或三垂线定理的逆定理”证明线线垂直问题.考查了异面直线所成角问题.还利用了余弦定理求角度,注意异面直线所成角范围是(0,π],这是易错点.属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{5}{4}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “p∧q”为真 | B. | “p∨q”为假 | C. | p真q假 | D. | p假q真 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | b<a<c | C. | a<c<b | D. | a<b<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com