
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
分析 由条件判断各个选项中的函数是否是偶函数,从而得出结论.
解答 解:由于①y=($\sqrt{x}$)2的定义域为[0,+∞),不关于原点对称,故该函数不是偶函数,故它的图象不关于y轴对称,故排除①.
由于②y=x3,是奇函数,它的图象关于原点对称,故排除②.
由于③y=f(x)=2|x|的定义域为R,且满足f(-x)=f(x),故它是偶函数,故它的图象关于y轴对称,故③满足条件.
由于④y=$\frac{2}{{x}^{2}}$的定义域为R,且满足f(-x)=f(x),故它是偶函数,故它的图象关于y轴对称,故④满足条件.
故选:D.
点评 本题主要考查函数的奇偶性的判断,函数的奇偶性的性质,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一段图象如图所示,
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的一段图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (-∞,-2] | C. | (-∞,-4) | D. | (-∞,-4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
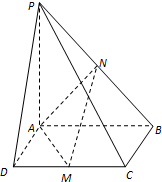 如图:已知四棱锥P-ABCD,底面是边长为6的正方形ABCD,PA=8,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM、AN、MN.
如图:已知四棱锥P-ABCD,底面是边长为6的正方形ABCD,PA=8,PA⊥面ABCD,点M是CD的中点,点N是PB的中点,连接AM、AN、MN.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com