
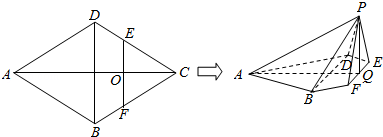
分析 (1)证明PO⊥BD,AO⊥BD,然后利用直线与平面垂直的判定定理证明即可;
(2)建立空间坐标系,求出平面的法向量,利用向量法即可求二面角B-AP-O的正切值.
解答 证明:(1)因为平面PEF⊥平面ABD,平面PEF∩平面ABD=EF,PO?平面PEF,
∴PO⊥平面ABD
则PO⊥BD,又AO⊥BD,AO∩PO=O,AO?平面APO,PO?平面APO,
∴BD⊥平面APO,(6分)
(2)以O为原点,OA为x轴,OF为y轴,OP为z轴,建立坐标系,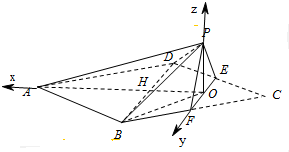
则O(0,0,0),A(3$\sqrt{3}$,0,0),P(0,0,$\sqrt{3}$),B($\sqrt{3}$,2,0),…(8分)
设$\overrightarrow{n}$=(x,y,z)为平面OAP的一个法向量,
则$\overrightarrow{n}$=(0,1,0),$\overrightarrow{m}$=(x,y,z)为平面ABP的一个法向量,
$\overrightarrow{AB}$=(-2$\sqrt{3}$,2,0),$\overrightarrow{AP}$=(-3$\sqrt{3}$,0,$\sqrt{3}$),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AB}=0}\\{\overrightarrow{m}•\overrightarrow{AP}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{-2\sqrt{3}x+2y=0}\\{-3\sqrt{3}x+\sqrt{3}z=0}\end{array}\right.$,
令x=1,则y=$\sqrt{3}$,z=3,
则$\overrightarrow{m}$=(1,$\sqrt{3}$,3)….(10分)
cosθ=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{\sqrt{3}}{\sqrt{13}}$,
∴tanθ=$\frac{\sqrt{30}}{3}$…..(12分)
点评 本题主要考查线直线垂直的判定以及二面角的应用,建立坐标性,求出平面的法向量,利用向量法是解决本题的关键.综合性较强.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “p∧q”为真 | B. | “p∨q”为假 | C. | p真q假 | D. | p假q真 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | 1 | C. | -$\frac{\sqrt{2}}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
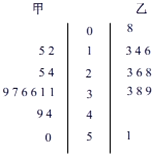 如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.则甲、乙两名运动员成绩比较( )
如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.则甲、乙两名运动员成绩比较( )| A. | 甲比乙稳定 | B. | 乙比甲稳定 | ||
| C. | 甲、乙稳定程度相同 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | b<a<c | C. | a<c<b | D. | a<b<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com