
分析 由题意,作出点E关于面ABCD的对称点E′,连C1E′交面ABCD于点F,则C1E′的长即为所求.
解答 解:由题意,作出点E关于面ABCD的对称点E′,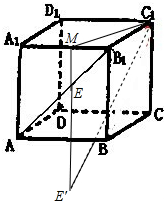
连C1E′交面ABCD于点F,
则C1E′的长即为所求.
∵E是AB1的中点,
∴C1E′=$\sqrt{1+\frac{1}{4}+(1+\frac{1}{2})^{2}}$=$\frac{\sqrt{14}}{2}$.
∴EF+FC1的最小值为$\frac{\sqrt{14}}{2}$.
故答案为:$\frac{\sqrt{14}}{2}$.
点评 本题考查多面体和旋转体表面上的最短距离问题,作出点E关于面ABCD的对称点E′,确定C1E′的长即为所求是关键.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{19}{36}$ | B. | $\frac{11}{36}$ | C. | $\frac{7}{12}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c>a>b | B. | a>b>c | C. | b>c>a | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
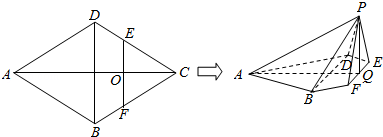
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+(y-1)2=$\sqrt{2}$ | B. | (x+1)2+(y+1)2=$\sqrt{2}$a | C. | (x+a)2+(y+a)2=2a2 | D. | (x-a)2+(y-a)2=2a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
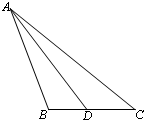 在△ABC中,角A,B,C所对的边分别为a,b,c,且sin2A+sin2C=sin2B-sinAsinC.
在△ABC中,角A,B,C所对的边分别为a,b,c,且sin2A+sin2C=sin2B-sinAsinC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com