
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 由x1=$\frac{1}{3}$,xn+1=xn2+xn,可得$\frac{{x}_{n+1}}{{x}_{n}}$=xn+1>1,因此数列{xn}单调递增,可得x4=$\frac{52}{81}$×$(\frac{52}{81}+1)$>1,于是当n≥4时,xn>1,0<1-$\frac{1}{{x}_{2017}}$<1.由xn+1=xn2+xn,可得$\frac{1}{{x}_{n}}$-$\frac{1}{{x}_{n+1}}$=$\frac{1}{{x}_{n}+1}$.利用“裂项求和”方法即可得出.
解答 解:由x1=$\frac{1}{3}$,xn+1=xn2+xn,可得$\frac{{x}_{n+1}}{{x}_{n}}$=xn+1>1,
∴数列{xn}单调递增,可得x2=$\frac{4}{9}$,x3=$\frac{52}{81}$,x4=$\frac{52}{81}$×$(\frac{52}{81}+1)$>1,
∴当n≥4时,xn>1.
∴0<1-$\frac{1}{{x}_{2017}}$<1.
∵xn+1=xn2+xn,∴$\frac{1}{{x}_{n}}$-$\frac{1}{{x}_{n+1}}$=$\frac{1}{{x}_{n}+1}$.
∴和数$\frac{1}{{1+{x_1}}}+\frac{1}{{1+{x_2}}}+\frac{1}{{1+{x_3}}}+…\frac{1}{{1+{x_{2016}}}}$=$(\frac{1}{{x}_{1}}-\frac{1}{{x}_{2}})$+$(\frac{1}{{x}_{2}}-\frac{1}{{x}_{3}})$+…+$(\frac{1}{{x}_{2016}}-\frac{1}{{x}_{2017}})$=3-$\frac{1}{{x}_{2017}}$=2+1-$\frac{1}{{x}_{2017}}$的整数部分的值为2.
故选:C.
点评 本题考查了数列递推关系、“裂项求和”方法、数列单调性,考查了推理能力与计算能力,属于中档题


科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | c<a<b | C. | b<c<a | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “p∧q”为真 | B. | “p∨q”为假 | C. | p真q假 | D. | p假q真 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 星期x | 1 | 2 | 3 | 4 | 5 |
| 需求量y(单位:kg) | 236 | 246 | 257 | 276 | 286 |
| 时间代号t | -2 | -1 | 0 | 1 | 2 |
| z | -21 | -11 | 0 | 19 | 29 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
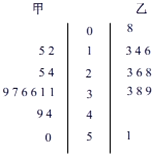 如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.则甲、乙两名运动员成绩比较( )
如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图.则甲、乙两名运动员成绩比较( )| A. | 甲比乙稳定 | B. | 乙比甲稳定 | ||
| C. | 甲、乙稳定程度相同 | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com