练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
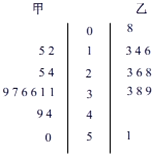
    6．如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图．则甲、乙两名运动员成绩比较（　　）
    A．甲比乙稳定B．乙比甲稳定
    C．甲、乙稳定程度相同D．无法确定

    分析 计算甲，乙的方差，根据方差的大小判断．

    解答 解：$\overline{{x}_{甲}}$=$\frac{1}{13}$（12+15+24+25+31+31+36+36+37+39+44+49+50）=33，
    $\overline{{x}_{乙}}$=$\frac{1}{11}$（8+13+14+16+23+26+28+33+38+39+51）=$\frac{289}{11}$≈26.3，
    ∴S2甲=$\frac{1}{13}$[212+182+92+82+22+22+32+32+42+62+112+162+172]=127.23．
    S2乙=$\frac{1}{11}$[（8-26.3）2+（13-26.3）2+（14-26.3）2+（16-26.3）2+（23-26.3）2+（26-26.3）2+（28-26.3）2+（33-26.3）2+（38-26.3）2+（39-26.3）2+（51-26.3）2]=157.84．
    ∵S2甲＜S2乙，
    故甲的成绩比乙的成绩稳定，
    故选：A．

    点评 本题考查了茎叶图，数据的方差与茎叶图的关系，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    16．已知ab＜0，则$\frac{b}{a}$+$\frac{a}{b}$的取值范围是（　　）
    A．（-∞，-2）B．（-∞，-2]C．（-∞，-4）D．（-∞，-4]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．数列{xn}满足：x1=$\frac{1}{3}$，xn+1=x${\;}_{n}^{2}$+xn，则下述和数$\frac{1}{{1+{x_1}}}+\frac{1}{{1+{x_2}}}+\frac{1}{{1+{x_3}}}+…\frac{1}{{1+{x_{2016}}}}$的整数部分的值为（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．设a=30.1，b=logπ2，c=log2sin$\frac{2π}{3}$．则（　　）
    A．c＞a＞bB．a＞b＞cC．b＞c＞aD．c＞b＞a

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．如图所示，在边长为4的菱形ABCD中，∠DAB=60°，点E，F分别是边CD，CB的中点，EF∩AC=O，沿EF将△CEF翻折到△PEF，连接PA，PB，PD，得到五棱锥P-ABFED，且AP=$\sqrt{30}$，PB=$\sqrt{10}$．
    （1）求证：BD⊥平面POA；
    （2）求二面角B-AP-O的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．下列关于等高条形图的叙述正确的是（　　）
    A．从等高条形图中可以精确地判断两个分类变量是否有关系
    B．从等高条例形图中可以看出两个变量频数的相对大小
    C．从等高条形图可以粗略地看出两个分类变量是否有关系
    D．以上说法都不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．圆心为（a，a）（a≠0）且过原点的圆的方程是（　　）
    A．（x-1）2+（y-1）2=$\sqrt{2}$B．（x+1）2+（y+1）2=$\sqrt{2}$aC．（x+a）2+（y+a）2=2a2D．（x-a）2+（y-a）2=2a2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知α是第三象限角，sinα=-$\frac{5}{13}$，则cosα=（　　）
    A．-$\frac{5}{13}$B．-$\frac{12}{13}$C．$\frac{5}{13}$D．$\frac{12}{13}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．若关于x的不等式2${\;}^{{x}^{2}-ax}$＞（$\frac{1}{2}$）2a在实数集上恒成立，则实数a的取值范围（0，8）．

    查看答案和解析>>

    同步练习册答案